Un modelo de Opciones Reales y Teoría de Juegos para valuar acuerdos estratégicos y penalidades
A Real Options and Games Theory model for valuing strategic commitment and penalties
Gastón S. Milanesi
Universidad Nacional del Sur (Argentina)
https://orcid.org/0000-0003-1759-6448
RESUMEN
Las decisiones estratégicas de inversión de equipos y recursos humanos, para la prestación de servicios especializados presentan barreras de salida y altos costos transaccionales. Implica una exposición a múltiples fuentes de incertidumbre. Su análisis y valuación requiere de modelos basados en Opciones Reales y Juegos. Motivado en ello, se propone un modelo para valorar contratos estratégicos de prestación de servicios de alta especificidad. Este dentro del marco de las opciones reales simples y juegos (SROG). Su funcionamiento es explorado y analizado aplicando la metodología de análisis de casos en administración. Para ello se utiliza los contratos de servicios formales e informales de análisis de agente sostén, en las perforaciones no convencionales de shale. Desde la perspectiva del proveedor del servicio, el modelo es aplicado y adaptado a valorar corriente de pagos contingentes derivados de las estrategias; resultados no óptimos producto de no acordar formalmente y el valor de la opción de intercambio. En los casos de acuerdos formales de suministro permite cuantificar las sanciones económicas por incumplimiento desde una perspectiva de SROG. Finalmente, se concluye enunciado su alcances y limitaciones.
PALABRAS CLAVE
Opciones Reales; Teoria de Juegos; Estrategias; Penalidades.
ABSTRACT
Strategic decisions regarding investments in equipment and human resources for the provision of specialized services present exit barriers and high transactional costs. They involve exposure to multiple sources of uncertainty. Their analysis and valuation require models based on Real Options and Game Theory. Motivated by this, a model is proposed to value strategic contracts for the provision of highly specific services, within the framework of simple real options and games (SROG). Its functioning is explored and analyzed using case study methodology in management. For this, formal and informal service contracts of supporting agent analysis are utilized in unconventional shale drilling. From the perspective of the service provider, the model is applied and adapted to value streams of contingent payments derived from strategies, suboptimal outcomes due to the lack of formal agreements, and the value of the exchange option. In the cases of formal supply agreements, it allows for quantifying economic penalties for non-compliance from an SROG perspective. Finally, conclusions are drawn regarding its scope and limitations.
KEYWORDS
Real Options; Games Theory; Strategies; Penalties.
Clasificación JEL: G13, G31.
MSC2010: 91A99.
1. Introducción
La valuación financiera de acuerdos económicos demanda el uso de modelos numéricos con capacidad para estimar fuentes de riesgo como: a) el valor actual de flujos de fondos estocásticos producto de la flexibilidad estratégica derivada de las inversiones de la empresa; b) la exposición a la incertidumbre producida por las potenciales conductas de los agentes. En relación a la última fuente de riesgo, la empresa disminuye su grado de exposición a la incertidumbre a través de cláusulas acordadas en los contratos. El costo de la cobertura contractual reside en la pérdida de flexibilidad estratégica. No obstante, las ventajas de los contratos, particularmente aquellos diseñados para proteger inversiones en activos específicos, reside en la reducción de los costos de transacción. Esto es así, debido a que las cláusulas económicas de los contratos tienen por objeto brindar cobertura a las inversiones y flujos de fondos esperados, generados por activos altamente especializados. El Análisis de los Costos de Transacción (TCA), se caracteriza por construir un marco normativo cuyo objetivo principal consiste en el diseño de mecanismos eficientes de cobertura aplicables a las relaciones económicas, (Williamson, 1983; 1985). Todo contrato que implique transacciones económicas contiene costos asociados. Estos emergen de negociar, formalizar e inducir el cumplimiento de los acuerdos por los agentes intervinientes con el objeto de mitigar riesgos. La teoría identifica tres grupos de fuentes de riesgo que generan como resultado costos de transacción:
a)Racionalidad limitada: supone que los agentes tienen capacidad limitadas para obtener y procesar información, restringiendo sus habilidades para la toma de decisiones individuales.
b)Incertidumbre general del sistema: ocasionada principalmente por el comportamiento intencionado de los agentes. Es acentuada por el contexto de negocios donde se desenvuelve la firma (la economía, el sector productivo de pertenencia, tecnología, entre otros.), contribuyendo a generar mayor incertidumbre a la toma de decisiones.
c)Especificidad de las transacciones: implica que el valor de la opción de abandono para inversiones en activos fijos altamente especializados y específicos, es nulo o negativo. Consecuentemente demanda recaudos extras para una mayor protección en la forma de penalidades económicas frente al incumplimiento.
De todas las fuentes de riesgo citadas, la existencia de inversiones en activos específicos y la persistencia de la incertidumbre, quizá sean los factores más significativos a considerar para el diseño y valoración de relaciones contractuales. La incertidumbre proveniente del contexto nace de los eventos propios del mercado y de los avances tecnológicos. En determinados sectores, la especificidad de la actividad hace que la inversión en activos fijos y tecnología requerida para prestar el servicio o proveer el insumo, la transforme en irreversible, con nulo valor de la opción de abandono. Adicionalmente, considerando el poder de negociación de los agentes, existe el riesgo potencial de apropiación por la contraparte del valor actual de la corriente de beneficios netos generados por el activo especifico (Kein, Crawford, y Alchain, 1978). Sin acuerdo formal, los costos transaccionales son mitigados con estrategias de integración vertical, cuyo impacto esta en brindar cobertura contra la incertidumbre (Heide y Stump, 1995). Los modelos tradicionales solamente basados en el análisis de costos transaccionales, se caracterizan por ser estáticos. Se concentran en el estudio y análisis de las conductas maliciosas de los agentes. No consideran los potenciales beneficios y posibilidades de la flexibilidad estratégica, derivada de las oportunidades que genera el comportamiento dinámico del mercado. Una segunda generación de modelos, incorporan el enfoque de opciones reales explorando las consecuencias de los acuerdos contractuales en la cobertura de riesgos de mercado y tecnológico (Argyres y Liebeskind, 1999; 2000); (Barney y Lee, 2000) y acuerdos de suministro y nuevas oportunidades de negocio (Rese y Roemer, 2004).
La valoración de relaciones contractuales, costos de transacción y valor económico de las decisiones requiere del planteo de modelos integrales. Deben tener la capacidad de predecir el valor esperado de la relación contractual, derivada de los potenciales cursos de acción de las partes intervinientes. En paralelo, debe ser capaz de calcular las penalidades económicas en el caso de conducta maliciosa, incentivando el cumplimiento de las clausulas acordadas. Por ello, los contratos económicos pueden asimilarse a un “juego”, donde la elección de la mejor estrategia será una función de su valor intrínseco, ajustado a las posibles respuestas los agentes que interactúan entre sí (Nash, 1953).; Kreps, D. (1982) Guintis, H. (2009). Los modelos a ser utilizados encuentran su marco teórico en la Teoría de Opciones Reales y Teoría de Juegos. La primera proporciona el marco conceptual para valorar la flexibilidad estratégica contenida en las decisiones de inversión. La Teoría de Opciones Reales solo considera dos fuentes de incertidumbre: riesgo de las decisiones de los agentes y de los estados de la naturaleza. En estos modelos, las acciones de los terceros son consideradas como variables pasivas, con un comportamiento dado. El de los pagos contingentes se enriquece a partir de su asociación con la Teoría de Juegos. Esta brinda el marco teórico para modelar las potenciales conductas, sobre la base de soluciones de equilibrio. El resultado de conjugar ambas teorías brinda como resultado un conjunto de modelos. Siguiendo a Smit y Trigeorgis, (2004) se clasifican en:
a)Modelos Simples de Teoría de Juego y Opciones Reales (SROG, standard real options games): los primeros trabajos corresponden a (Smit y Ankum, 1993); (Dixit y Pindyck, 1994); (Grenadier, 1996); (Kulatilaka y Perotti, 1998); (Smit, 2003), (Chevalier-Roignant, y Trigeorgis, 2013). entre otros. En estos modelos el valor de la inversión asume un comportamiento aleatorio, (por lo general geométrico y aritmético browniano con modificaciones). El proceso es planteado de manera discreta y los agentes asumen una conducta neutral al riesgo. El costo de la inversión es hundido y cierto. Analizado el curso de acción y valorado mediante modelos de opciones, seguidamente es planteada la interacción estratégica entre los competidores, aplicando soluciones de equilibrio que permitan anticipar y explicar conductas. En estos juegos, las acciones cooperativas permiten acceder situaciones superiores, comparados con los resultados derivados de juegos de suma cero (Axelrod, 1986). Implica la promoción de acuerdos estratégicos, estableciendo penalizaciones que promuevan incentivos de cumplimiento (Milanesi y Thomé, 2015), (Zapata Quimbayo, 2020); (Milanesi, 2021), (Milanesi, 2023a, 2023b).
b)Modelos Complejos de Teoría de Juegos y Opciones Reales (NSROG, non-standard real options games). Presentan dos o más variables estocásticas, y las decisiones no se toman en un punto del tiempo determinado. Conjugan modelos microeconómicos de estructuras de mercados con opciones de salidas, asimetrías entre firmas, estructuras informativas (perfectas/imperfectas), cooperación entre firmas, participaciones en el mercado, entre otras situaciones de mercado-competencia. Se pueden citar trabajos como los de (Ghemawat y Nalebuff, 1985); (Fudenberg y Tirole, 1985); (Lambrecht, 2001); (Grenadier, 2000); (Grenadier, 2002); (Paxson y Pinto, 2003); (Murto, 2004); (Pawlina y Kort, 2006); (Hsu y Lambrecht, 2007); (Armada, Kryzanowski y Pereira, 2009); (Thijssen, 2010); (Graham, 2011); (Boyer, Laserrere y Moreaux, 2012); (Chevalier-Roignant y Trigeorgis, 2013); (Azevedo y Paxson, 2014); (Ebina, Matsushima y Nishide, 2022); (Yu, Wen, Huberts, y Kort, 2024) entre otros.
Los modelos basados en Opciones Reales y Teoría de Juegos tienen la capacidad de incorporar factores intrínsecos y exógenos derivados de las fuentes de incertidumbre a la que se exponen las partes. En tal sentido, en el marco de los simples modelos de opciones reales y teoría de juegos (SROG), se propone una alternativa destinada a valuar decisiones estratégicas de inversión, en particular, de alta especialización para la prestación de servicios específicos. Estas se caracterizan por sus desventajas competitivas producto de las significativas barreras de salida del negocio y poca reversión (nulo o bajo valor de la opción de abandono). Los altos costos transaccionales toman la forma de múltiples fuentes de incertidumbre, como la evolución de la demanda (estado de la naturaleza), la decisión de acordar precios y proponer contratos de suministros (decisión de la empresa) y la conducta de los agentes e incentivos para el cumplimiento a partir del riesgo de no provisión y aplicación de multas (cliente). Desde la perspectiva del proveedor el modelo permite su aplicación y adaptación para cuantificar: (a) el valor actual de la corriente de pagos contingentes asociados a cada estrategia; (b) las consecuencias de no acordar, formalmente traducidas en un equilibrio subóptimo; (c) el valor añadido por la colaboración formal (acuerdo empresarial), reforzado en los incentivos al cumplimiento manifestado en el valor de las sanciones económicas. Específicamente es analizado un caso sobre la prestación de servicios de análisis de agente de sostén, en las perforaciones no convencionales de shale complejo Vaca Muerta, Argentina. La estructura del trabajo es la siguiente: en primer lugar, se desarrollado y fundamentado el modelo numérico de valoración de flujos contingentes y penalidades económicas, basado en un enfoque SROG. Aplicando la metodología de estudio de casos en administración (Castro Monge, 2010), se ilustra y analiza aportes y limitaciones del modelo. Para ello se estudia las relaciones derivadas de contratos de servicio de análisis, correspondientes al agente sostén en exploraciones no convencionales de shale, en el área geográfica Vaca Muerta, Neuquén Argentina. Desde la perspectiva del proveedor del servicio, el modelo permite valorar los flujos asociados de acuerdos formales de provisión con su correspondiente multa y la penalidad económica ante el incumplimiento. En situaciones de acuerdos incorpora el análisis del valor correspondiente a la opción de intercambio de clientes. Informa las estrategias dominantes y el equilibrio débil, propias de las conductas de las partes (proveedor-cliente). Finalmente son expuestas las principales conclusiones y limitaciones del enfoque.
2. Modelo: Valor de los pagos contingentes y penalidades en contratos de suministro.
La presente sección desarrolla el modelo de opciones reales adaptado a la valoración de acuerdos contractuales. La primera parte expone las ecuaciones básicas del modelo binomial para valorar opciones reales. Seguidamente, este es adaptado a la valuación de comportamientos estratégicos en situaciones de contratos económicos.
2.1. El modelo binomial
El modelo binomial (Cox, Ross y Rubinstein, 1979), (Chance, 2008); constituye la alternativa de mayor difusión para valorar opciones reales en tiempo discreto. Uno de los principales insumos para construir el modelo está dado por la medida de volatilidad del subyacente (σ), el cual referencia los riesgos del modelo, en el caso de un solo estado (Milanesi, 2023a). En opciones reales el subyacente es representado por el flujo o valor de la inversión. La volatilidad permite estimar las variables del modelo binomial: coeficientes de ascenso, descenso (ecuación 1) y probabilidades neutrales al riesgo (ecuación 2).
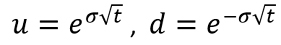
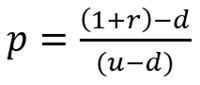
El valor recursivo de la opción se plantea mediante la siguiente ecuación general,
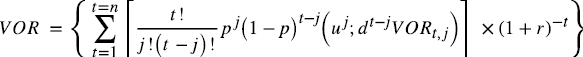
Donde, VOR representa el valor actual de la opción,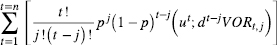 
, la combinatoria correspondiente a los coeficientes equivalentes ciertos para cada periodo (t hasta n) en cada nodo (j), 
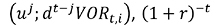el factor de actualización. Cabe destacar que la presente expresión genérica, plantea el ejercicio en cada uno de los periodos de tiempo. En el supuesto de ejercicio en un periodo específico, la expresión queda planteada como,
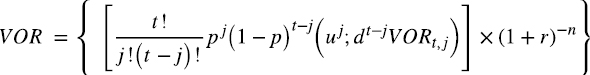
2.2. Adaptación del modelo binomial a la valoración de acuerdos contractuales cliente -proveedor.
El modelo desarrollado en el apartado anterior se caracteriza por su simplicidad y versatilidad para valorar pagos contingentes derivados de estrategias y acuerdos empresariales. En la presente sección el modelo será adaptado a la valoración de un acuerdo de provisión desde la perspectiva del cliente y el proveedor. El flujo de beneficios esperados sigue un proceso binomial determinado por un comportamiento estocástico de las cantidades demandadas (ecuación 4). Los precios se mantienen estables, una vez acordados, en t=0.
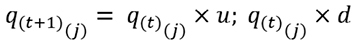
Uno de los principales supuestos del modelo y, al mismo tiempo simplificación, reside en el comportamiento estocástico asignado a la demanda. El riesgo de mercado y el tecnológico son explicados íntegramente por la mediad de volatilidad, expresada en el desvío estándar. Otro de los supuestos reside en el uso de probabilidades neutrales al riesgo. Implica asumir normalidad en la distribución de probabilidad, empleando dos momentos estocásticos (media y desvío) para explicar el comportamiento de la variable aleatoria (cantidades demandadas). Implica ajustar por riesgo en los flujos y evitan el uso de tasas ajustadas por riesgo en el proceso de descuento, evitando el error en el cual se incurre en valuación con los árboles de decisión (Copeland y Antikarov, 2001).
2.1.1 Pagos contingentes sin acuerdo formal.
Surge del producto entre las cantidades demandadas (ofertadas), el flujo de fondos para cada parte contratante y la probabilidad técnica de que el cliente proceda a contratar. Las siguientes expresiones manifiestan el valor actual de los pagos contingentes para proveedor y cliente
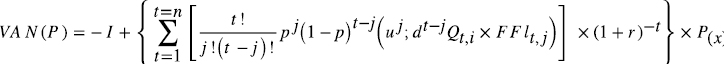
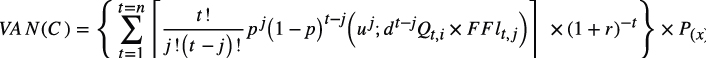
En las ecuaciones precedentes, VAN(P) y VAN(C) representan el valor actual de los flujos correspondientes al proveedor-cliente respectivamente. La inversión inicial se representada por la variable –I, u, d y p son los parámetros del modelo binomial (ecuaciones 1, 2 y 3). El producto entre cantidades proyectadas (ecuación 4) y flujo de fondos libres correspondiente a cada instancia de negociación, está dado por Qt,j×FFlt,i. Finalmente, r representa a la tasa libre de riesgo y P(x) las probabilidades constantes de respetar el acuerdo informal y contratar. Si no existe acuerdo formal, se supone que el proveedor no tiene flexibilidad estratégica de abandono dada la especificidad de la inversión en equipos y formación de capital humano. Tiene la posibilidad de ejercer la opción de intercambio de clientes (ecuación 7), al no asumir compromiso formal de provisión.
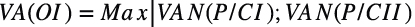
Donde VA(OI) representa el valor de la opción de intercambio. Este es máximo entre el valor actual de contratar con el cliente I o II (ecuación 6). El ejercicio de opción se presenta en los casos donde no existe acuerdo contractual formal con penalidades. En estos casos, el excedente sobre costos a favor de cliente-proveedor, es distribuido, acorde al poder de negociación.
El precio es acordado para el proveedor es: pt=vn-(vn-cn )×%ff y para el cliente es: pt=cn-(vn-cn )×%ff. Donde el cliente toma como referencia vn (el precio de transferencia interno o valor de costo) y el proveedor cn , siendo el costo variable del servicio. La variable %ff, representa la fracción del resultado que se apropia cliente – proveedor en el proceso de negociación. En teoría de juegos, sin acuerdo, el precio surge de un escenario con equilibrio de pánico (panic equilibrium)
2.1.2 Pagos contingentes con acuerdo contractual.
El valor actual de los pagos contingentes surge de aplicar las ecuaciones 5 y 6 sin considerar las probabilidades técnicas de contratación. Existe certeza en materia de prestación–demanda de servicio P(x)= 1. Además, el precio surge de un acuerdo formal, producto de un equilibrio colaborativo de Nash, siendo esta la estrategia dominante. El incentivo para reforzar las conductas de colaboración se refuerza con multas monetarias frente al incumplimiento.
2.1.3 Valor de la penalidad para el proveedor
El valor de la multa (ecuación 8) surge del máximo valor entre el perjuicio que origina en la contraparte (valor actual de los flujos de fondos para el cliente con acuerdo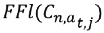 
y los beneficios potenciales a su favor. La conducta de incumplimiento implica que el proveedor contrata con el cliente alternativo. Consecuentemente, el beneficio potencial estará dado por,
,
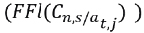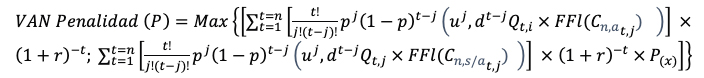
2.1.4 Valor de la penalidad para el cliente
Surge de no respetar el precio acordado, y forzando al proveedor a cumplir a un precio sin acuerdo (ecuación 9). El valor de la multa es el máximo entre el valor actual para el proveedor correspondientes a flujos de fondos con precios acordados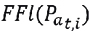 
; y el valor actual de flujos de fondos sin precios acordados,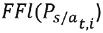 
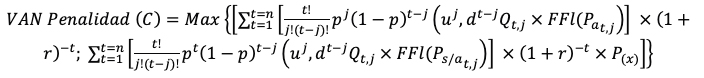
Para el cliente, en la mayoría de los casos el valor de la penalidad es explicado por el perjuicio originado al proveedor y no por su beneficio potencial.
3. Metodologia: Aplicación del modelo SROG sobre contratos de prestación de servicios.
Metodológica se utiliza en el análisis de caso en administración (Castro Monge, 2010), con el fin de examinar e ilustrar las interrelaciones entre las variables y posibles resultados del modelo. Es estudiado la inversión incremental en un laboratorio de estudios de arenas o agentes de sostén (proppants) en el reservorio Vaca Muerta, Neuquén, Argentina. La especificidad de los equipos y de los procesos de capacitación hace que la inversión se caracterice por sus altas barreras de salidas, tornando irreversible y poco líquida en caso de fracasar la unidad de negocio en la cual aplica. En la etapa de estimulación de un pozo no convencional (shale) de crudo, la arena como agente de sostén representa una fracción significa del costo de inversión (Peñaranda, 2014); (Giglio, M. 2018). En la composición agregada de costos el agente de sostén se ubica dentro de los conceptos que conforman el CAPEX (etapa de inversión de capital). El objeto de la prestación del servicio de laboratorio de arenas reside en analizar y asegurar la calidad del agente de sostén. Las instancias del proceso en las cuales se requiere el análisis de arenas son las siguientes: a) al momento de licitar compras, b) una vez adquirida las arenas, c) búsqueda de zonas con reservas de agentes de sostén. El caso a ser analizado versa sobre la alternativa b); puesto que es el más frecuente, rutinario y de mayor impacto económico.
Las cantidades demandas del servicio de análisis de arenas es función directa de la evolución de explotación de shale. Específicamente, existe una relación directa entre etapas de fractura y uso de agente sostén. Mayor cantidad de fracturas implica de parte de los clientes mayor demanda de agente sostén, que se traduce en una mayor demanda de análisis sobre calidad.
Partiendo de los datos e información obtenidos de los sitios web Ministerio de Energía y Recursos Naturales de la Provincia de Neuquén, Argentina; Experto en Shale y Más Energía, se construye;
Tabla 1: Evolución fracturas y demanda agente sostén:
|
Periodos (*) |
Fracturas totales |
Toneladas totales |
Muestras (**) |
Camiones (***) |
|
2024 |
18259 |
4.564.800,00 |
25.360 |
152.160 |
|
2023 |
14747 |
3.686.750,00 |
20.482 |
122.892 |
|
2022 |
12522 |
3.130.500,00 |
17.392 |
104.350 |
|
2021 |
10254 |
2.563.500,00 |
14.242 |
85.450 |
Fuente: elaboración propia. (*) periodo 2024: al mes de mayo acumulaba 7608 fracturas, anualizadas 18.529; (**) Muestras son obtenidas a partir del total de toneladas totales, las cuales surgen del producto entre fractura y demanda de arena (250 toneladas). Las normas ISO 13503-2 exigen 1 tonelada cada nueve, y sobre dicha población, la cantidad de muestras representa el 5 %. (***) Se asume que transportan 30 toneladas promedio.
De la tabla 1 se obtiene la serie de variaciones logarítmicas, calculadas como el cociente entre la cantidad de muestras practicadas en los periodos t y t-1,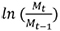 
. El factor que impulsa la demanda del servicio de análisis son las fracturas. Dado lo limitado de la serie de tiempo en función a que el reservorio es de reciente data, la volatilidad fue estimada empleando simulación Monte Carlo, utilizando simulación Montecarlo (Brandao, Dyer y Hahn, 2005 y 2012); (Godinho, 2006 y 2015) (Pareja Vasseur, Prada Sánchez y Moreno Escobar, 2019). Se supone un comportamiento aleatorio de las fracturas siguiendo un comportamiento estocástico con distribución uniforme. De las iteraciones realizadas sobre la serie de la tabla 1 se obtiene una medida de volatilidad promedio del σ=14,07%.
La inversión inicial requerida para montar el laboratorio de arena es de u$1.450.000. La inversión presenta alto riesgo habida cuenta su alta barrera de salida o irreversibilidad. Los costos variables (cv) por muestra ascienden a u$500, integrando los costos directos e indirectos correspondiente al servicio de inspección.
Del lado de la demanda del servicio, existen dos clientes con diferentes participaciones mercado, en base a las concesiones otorgadas sobre territorio de exploración. El cliente (C1) posee una participación del 15 %, con un estimado sobre el periodo 2024 de 2739 fracturas. Implica una demanda inicial de 3804 análisis en adelante. El cliente (C2) posee una participación del 25 %, con un estimado sobre el periodo 2024 de 4564 fracturas. Resulta en una demanda inicial de 6340 análisis. La decisión de provisión, de parte del proveedor a los clientes, es mutuamente excluyente. El cliente (C1) inicia el proceso de contratación y presenta mayores probabilidades de concertar el acuerdo. La siguiente tabla se resumen las condiciones correspondientes a los clientes potenciales,
Tabla 2: Variables clientes I y II:
|
Cliente |
Cantidades |
Contrato (*) |
%(Beneficio) (**) |
|
Q (t=0) |
P(Cl) (x) |
FF (%) |
|
|
I |
3804 |
0,8 |
0,5 |
|
II |
6340 |
0,55 |
0,45 |
Fuente: elaboración propia. (*) probabilidad de contratar servicio sin acuerdo entre partes; (**) fracción del beneficio neto que se apropia el cliente en caso de no acuerdo.
En el caso de no firmar contrato, simplemente acordar la provisión del servicio informalmente (simple provisión del servicio), la tabla indica las probabilidades objetivas de contratación entre el cliente y proveedor (P(CI)x ). Asimismo, (%FF) representa la fracción de flujo de fondo neto apropiada por el cliente, al no acordar precio formalmente. Para esta situación, se presenta una apropiación de las ganancias en función al poder de negociación de las partes. En el caso del cliente I es del 50 %, mientras que cliente II se apropia del 45 % (situación de mayor ventaja para el proveedor). Se aprecia los perfiles cruzados, mientras que el cliente I presenta mayor compromiso de contratación se apropia de una fracción mayor de la ganancia, en relación al cliente II.
El primer proceso es el de negociación de precios. Implica considerar dos variables: valor de transferencia (vt) que el servicio tiene para el cliente y precio que deriva del acuerdo formal (Pt). Para el cliente el precio de transferencia representa el máximo valor que está dispuesto a pagar por el servicio, siendo incorporado como elemento del costo en su estructura. Consecuentemente, en el proceso de negociación son proyectados los siguientes escenarios:
a)Acuerdo formal (equilibrio): se pacta un precio de acuerdo (Pt) y define las bases para formalizar un acuerdo entre partes.
b)No acuerdo y fuerte poder de negociación del proveedor: este se apropia de la totalidad el beneficio, percibiendo como precio el valor de transferencia para el cliente (vt).
c)No acuerdo y fuerte poder de negociación del cliente: el cliente se apropie de la totalidad del beneficio, pagando como precio el costo variable del proveedor (cv).
d)No acuerdo y negociación (equilibrio de pánico): En este caso se llega a un precio sobre la base del beneficio que cada parte se apropia, en función a su poder de negociación (tabla 2).
Para el cliente I se suponen los siguientes valores correspondiente valor de transferencia, (vI)=u$1.200 y precio de equilibrio (pI)=u$1.000.
Para el cliente II se suponen los siguientes valores correspondiente a valor de transferencia (vII)=u$1.150 y precio de equilibrio (pII)=u$875.
Seguidamente se presentan las matrices correspondientes al juego con precios y flujos para cada cliente;
Tabla 3: Matriz cliente I precios – flujos de fondos
|
P |
C I |
|||
|
Acuerdo |
No acuerdo |
|||
|
Acuerdo |
$ 1.000,00 |
$ 1.000,00 |
$ - |
$ 500,00 |
|
$ 500,00 |
$ 200,00 |
$ - |
$ 700,00 |
|
|
No acuerdo |
$ 1.200,00 |
$ - |
$ 850,00 |
$ 850,00 |
|
$ 700,00 |
$ - |
$ 350,00 |
$ 350,00 |
|
Fuente: elaboración propia
La tabla expone la matriz de precios y flujos correspondiente a la relación cliente I – proveedor. Los recuadros superiores expresan precios, en itálicas se expone el flujo de fondos. Los pagos contenidos en la matriz presentan una foto determinística de la ecuación precio – costos para cada una de las partes. El precio de equilibrio es (pI=u$1.000), implica que la estrategia dominante (cliente I – proveedor) es no acordar imponiendo precio. De seguir dicha estrategia, el resultado implica que el cliente no percibe el servicio y el proveedor no tendría actividad. Sin acuerdo formal, el equilibrio de pánico deriva de la necesidad de negociar informalmente. El precio surge a partir de compartir beneficios sobre costos en función a sus fuerzas negociadoras. Conforme surge de la tabla 2, el porcentaje de beneficio apropiado por proveedor – cliente, para esta relación es del 50 %. En este caso, el precio para el proveedor es pp=vI-(vI-cV )×%ff y para el cliente es pV=CV-(vI-cV )×%ff, siendo este de u$850 por servicio. El flujo de fondos para ambas partes por unidad de servicio asciende a u$350. Para el cliente II se presenta la siguiente matriz,
Tabla 4: Matriz cliente II precios – flujos de fondos
|
P |
C II |
|||
|
Acuerdo |
No acuerdo |
|||
|
Acuerdo |
$ 875,00 |
$ 875,00 |
$ - |
$ 500,00 |
|
$ 375,00 |
$ 275,00 |
$ - |
$ 650,00 |
|
|
No acuerdo |
$ 1.150,00 |
$ - |
$ 792,50 |
$ 792,50 |
|
$ 650,00 |
$ - |
$ 357,50 |
$ 292,50 |
|
Fuente: elaboración propia
En relación al cliente II se exponen precios y flujos. En el caso de suscribir contrato de colaboración y suministro, el precio de acuerdo es de (pII=u$875). Sin acuerdo, no existe simetría en la apropiación del flujo de fondos. En este caso, el cliente accede al 45 % del flujo sobre el precio es pI=u$500+(u$1150-u$500)×0.45, obteniendo un flujo de beneficios a su favor de u$292,50. proveedor es pP=u$1150-(u$1150-u$500)×0,55, obteniendo un flujo de u$357,50.
4. Resultados
Son expuestos los resultados derivados de aplicar el modelo: valor estratégico de cada opción en situación con acuerdo y valor de la penalidad. Asimismo, el valor de los pagos contingentes sin acuerdo formal. Seguidamente es desarrollado el planteo extensivo y matricial del juego, proveedor-cliente, cuantificando los equilibrios en cada escenario.
4.1. Valor estratégico opción de intercambio y penalidades.
Para la proyección de las cantidades demandadas, se parte de la volatilidad estimada, de σ=14,07%, con coeficientes de ascenso (u=1,151), descenso (d=0,8687) y probabilidades neutrales al riesgo, (p=0,5711) (ecuaciones 1, 2 y 3). Partiendo de las cantidades de muestras en t=0 (tabla 2) son proyectadas las cantidades en un horizonte de cinco años (ecuación 4), donde la prestación del servicio comienza en t=1,
Tabla 5: Proceso binomial cantidades a demandar cliente I
|
0 |
1 |
2 |
3 |
4 |
5 |
|
3804 |
4379 |
5040 |
5802 |
6679 |
7688 |
|
3305 |
3804 |
4379 |
5040 |
5802 |
|
|
2871 |
3305 |
3804 |
4379 |
||
|
2494 |
2871 |
3305 |
|||
|
2167 |
2494 |
||||
|
1882 |
Fuente: elaboración propia
Tabla 6: Proceso binomial cantidades a demandar cliente II
|
0 |
1 |
2 |
3 |
4 |
5 |
|
6340 |
7298 |
8401 |
9670 |
11131 |
12813 |
|
5508 |
6340 |
7298 |
8401 |
9670 |
|
|
4785 |
5508 |
6340 |
7298 |
||
|
4157 |
4785 |
5508 |
|||
|
3611 |
4157 |
||||
|
3137 |
Fuente: elaboración propia
A continuación, son desarrollados los valores actuales correspondiente a la corriente de beneficios para el proveedor y clientes en situación con y sin acuerdo (ecuaciones 5 y 6). En el caso de acuerdo no formal, el valor de la flexibilidad estratégica es capturado por la opción de intercambio (cliente I y II) a favor del proveedor. Su ejercicio se realiza en t=1.
Los valores actuales constituyen los puntos de referencia para la toma de decisión y desarrollo del juego (ecuación 7). El resultado de las probabilidades neutrales al riesgo a partir de cálculo combinatorio es expuesto en la siguiente tabla.
Tabla 7: Probabilidades neutrales al riesgo
|
1 |
P |
2 |
P |
3 |
P |
4 |
P |
5 |
P |
|
1 |
57,11 % |
2 |
32,62 % |
3 |
18,63 % |
4 |
10,64 % |
5 |
6,08 % |
|
0 |
42,89 % |
1 |
48,99 % |
2 |
41,97 % |
3 |
31,96 % |
4 |
22,82 % |
|
∑ |
100 % |
0 |
18,39 % |
1 |
31,51 % |
2 |
36,00 % |
3 |
34,27 % |
|
∑ |
100,00 % |
0 |
7,89 % |
1 |
18,02 % |
2 |
25,73 % |
||
|
∑ |
100,00 % |
0 |
3,38 % |
1 |
9,66 % |
||||
|
∑ |
100,00 % |
0 |
1,45 % |
||||||
|
∑ |
100,00 % |
Fuente: elaboración propia
4.1.1 Valores Actual no formalización de acuerdo (Cliente I) (equilibrio de pánico)
Las siguientes ecuaciones estiman valores actuales por periodo y total para la relación contractual proveedor–cliente. Los valores correspondientes a flujos surgen de la matriz expuesta en la tabla 3, el proceso binomial (tabla 5) y las probabilidades neutrales al riesgo (tabla 7).
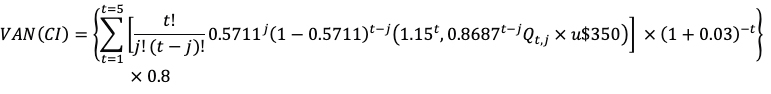
El valor por periodo surge de sumar en cada intervalo los valores correspondientes a los diferentes nodos. La sumatoria de los valores obtenidos actualizado al tipo sin riesgo, arroja el valor actual de la corriente de flujo de fondos. Finalmente, el valor actual total es ajustado por la probabilidad objetiva de contratacíón.
Tabla 8: Valor actual sin acuerdo formal compartiendo beneficio cliente I
|
VAN(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 3.875.600,00 |
$ 1.097.073,60 |
$ 1.129.985,81 |
$ 1.163.885,38 |
$ 1.198.801,94 |
$ 1.234.766,00 |
|
VAN(CI) |
1 |
2 |
3 |
4 |
5 |
|
$ 5.325.600,00 |
$ 1.097.073,60 |
$ 1.129.985,81 |
$ 1.163.885,38 |
$ 1.198.801,94 |
$ 1.234.766,00 |
Fuente: elaboración propia
4.1.2 Valores Actual no formalización de acuerdo (Cliente I) (apropiación total de beneficio)
Se exponen las expresiones y tablas correspondiente a la estimación del valor actual apropiándose cada parte de forma individual de la totalidad del beneficio,
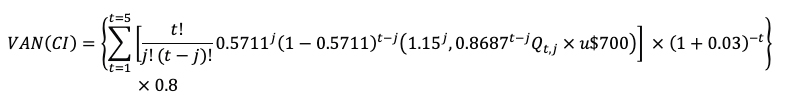
Tabla 9: Valor actual sin acuerdo formal apropiando la totalidad del beneficio cliente I
|
VAN(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 9.201.200,00 |
$ 2.194.147,20 |
$ 2.259.971,62 |
$ 2.327.770,76 |
$ 2.397.603,89 |
$ 2.469.532,00 |
|
VAN(CI) |
1 |
2 |
3 |
4 |
5 |
|
$ 6.657.000,00 |
$ 1.371.342,00 |
$ 1.412.482,26 |
$ 1.454.856,73 |
$ 1.498.502,43 |
$ 1.543.457,50 |
Fuente: elaboración propia
4.1.3 Valores Actual formalización de acuerdo (Cliente I) (equilibrio)
Las siguiente tabla y ecuaciones presenta el valor actual correspondiente a cada una de las partes en el supuesto de formalizar el acuerdo,
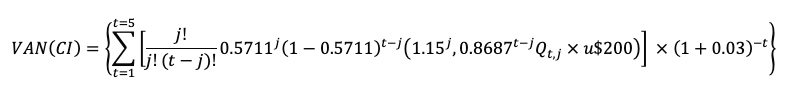
Tabla 10: Valor actual con acuerdo formal cliente I
|
VAN(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 8.060.000,00 |
$ 1.959.060,00 |
$ 2.017.831,80 |
$ 2.078.366,75 |
$ 2.140.717,76 |
$ 2.204.939,29 |
|
VAN(CI) |
1 |
2 |
3 |
4 |
5 |
|
$ 3.804.000,00 |
$ 783.624,00 |
$ 807.132,72 |
$ 831.346,70 |
$ 856.287,10 |
$ 881.975,72 |
Fuente: elaboración propia
En este escenario existe certeza en las prestaciones. La incertidumbre se manifiesta en la variación de las cantidades demandadas, las cuales dependen de la actividad de fractura. El incentivo para el cumplimiento reside en el establecimiento de penalidades económicas, calculadas a partir del flujo de pagos contingentes es el siguiente,
Tabla 11: Valores correspondientes a las penalidades cliente I
|
Penalidad(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 5.325.600,00 |
$ 1.097.073,60 |
$ 1.129.985,81 |
$ 1.163.885,38 |
$ 1.198.801,94 |
$ 1.234.766,00 |
|
Penalidad(CI) |
1 |
2 |
3 |
4 |
5 |
|
$ 9.510.000,00 |
$ 1.959.060,00 |
$ 2.017.831,80 |
$ 2.078.366,75 |
$ 2.140.717,76 |
$ 2.204.939,29 |
Fuente: elaboración propia
La penalidad representa el máximo valor entre el perjuicio ocasionado a la contraparte y el beneficio obtenido. Ante el incumplimiento, se supone que el cliente pierde el flujo de correspondiente al acuerdo formal o eventualmente el flujo del no acuerdo y provisión ajustada por la probabilidad de contratar.
4.1.4 Valores Actual no formalización de acuerdo (Cliente II) (equilibrio de pánico)
A partir del comienzo de la relación contractual compartiendo beneficios, el cliente se apropia del 45 % del beneficio. Las probabilidades de contratar con el proveedor son del 50 %. Los valores correspondientes a flujos, surgen de la matriz expuesta en la tabla 4 y el proceso binomial (tabla 6) y probabilidades neutrales al riesgo (tabla 7). El valor actual del flujo de fondos (ecuación 5 y 6) es el siguiente,
Tabla 12: Valor actual sin acuerdo formal compartiendo beneficio cliente II
|
VAN(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 4.216.375,00 |
$ 1.167.273,25 |
$ 1.202.291,45 |
$ 1.238.360,19 |
$ 1.275.511,00 |
$ 1.313.776,33 |
|
VAN(CII) |
1 |
2 |
3 |
4 |
5 |
|
$ 7.822.250,00 |
$ 1.910.083,50 |
$ 1.967.386,01 |
$ 2.026.407,59 |
$ 2.087.199,81 |
$ 2.149.815,81 |
Fuente: elaboración propia
4.1.5 Valores Actual no formalización de acuerdo (Cliente II) (apropiación total de beneficio)
Seguidamente se presentan las ecuaciones y tablas correspondiente a la estimación del valor actual, donde cada parte de manera unilateralmente se apropia de la totalidad del beneficio,
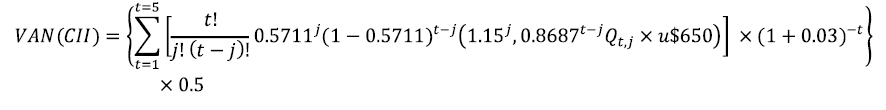
Tabla 13: Valor actual sin acuerdo formal apropiando la totalidad del beneficio cliente II
|
VAN(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 8.852.500,00 |
$ 2.122.315,00 |
$ 2.185.984,45 |
$ 2.251.563,98 |
$ 2.319.110,90 |
$ 2.388.684,23 |
|
VAN(CII) |
1 |
2 |
3 |
4 |
5 |
|
$ 4.121.000,00 |
$ 848.926,00 |
$ 874.393,78 |
$ 900.625,59 |
$ 927.644,36 |
$ 955.473,69 |
Fuente: elaboración propia
4.1.6 Valores Actual formalización de acuerdo (Cliente II) (equilibrio)
Si el acuerdo es formalizado, las expresiones y tablas para estimar el valor actual son las siguientes,
Tabla 14: Valor actual con acuerdo formal cliente II
|
VAN(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 10.437.500,00 |
$ 2.448.825,00 |
$ 2.522.289,75 |
$ 2.597.958,44 |
$ 2.675.897,20 |
$ 2.756.174,11 |
|
VAN(CII) |
1 |
2 |
3 |
4 |
5 |
|
$ 8.717.500,00 |
$ 1.795.805,00 |
$ 1.849.679,15 |
$ 1.905.169,52 |
$ 1.962.324,61 |
$ 2.021.194,35 |
Fuente: elaboración propia
Son calculadas las penalidades monetarias producto de la relación contractual con el cliente II (ecuaciones 8 y 9),
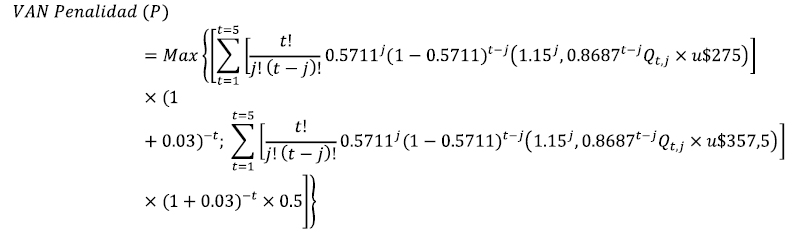
Tabla 15: Valores correspondientes a las penalidades cliente II
|
Penalidad(P) |
1 |
2 |
3 |
4 |
5 |
|
$ 9.161.300,00 |
$ 1.795.805,00 |
$ 1.967.386,01 |
$ 2.026.407,59 |
$ 2.087.199,81 |
$ 2.149.815,81 |
|
Penalidad(CII) |
1 |
2 |
3 |
4 |
5 |
|
$ 9.272.250,00 |
$ 1.910.083,50 |
$ 1.967.386,01 |
$ 2.026.407,59 |
$ 2.087.199,81 |
$ 2.149.815,81 |
Fuente: elaboración propia
4.1.7 Valores Actual no formalización de acuerdo. Opción de intercambio (equilibrio pánico) (Cliente I/II)
Sin acuerdo formal, existe la posibilidad para el proveedor de ejercer la opción de intercambio (ecuación 7), siendo
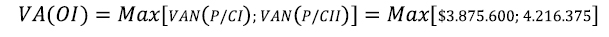
Tabla 16: Valor opción de intercambio para el proveedor
|
Decisión |
1 |
2 |
3 |
4 |
5 |
|
$ 4.216.375,00 |
$1.167.273,25 |
$1.202.291,45 |
$1.238.360,19 |
$1.275.511,00 |
$1.313.776,33 |
|
D@Max(I,II) |
II |
II |
II |
II |
II |
(Fuente: elaboración propia)
4.2. Planteo del juego. Resolución matricial y extensiva de las conductas contenidas en los acuerdos.
En la presente sección, son desarrolladas las matrices correspondientes a las estrategias de los agentes, abordadas desde la perspectiva del proveedor. Se plantean dos escenarios por clientes: formalización con penalidades o suministro sin acuerdo formal, y opción de intercambio. Los resultados obtenidos y expuestos en las tablas 8 a 16 constituyen el insumo, para estimar los valores actuales para el planteo del juego de forma extensiva y matricial.
4.2.1 Cliente I: Acuerdo formal con multa
Tabla 17: Expresiones relacionadas con las estrategias con acuerdo cliente I y proveedor
|
P |
C I |
|||
|
Cumple |
No cumple |
|||
|
Cumple |
V=VAN(P)c/a |
V=VAN(CI)c/a |
V=VA (indeminzación) + |
V=VAN(penalidad) CI- |
|
VOI (CII) sin acuerdo |
VAN(CI)s/a |
|||
|
No cumple |
V=VAN(penalidad) P- |
V=VA (indeminzación)- |
V=si(VOI(II/I>0;VOII(II),VO(I)) |
V=si(VOI(II/I>0; -(VA(I) s/a); |
|
VOI (CII) sin acuerdo=∆(VI-VII) |
VAN(CI)c/a |
VA(I)s/a-VA(I)c/a |
||
Fuente: elaboración propia
Tabla 18: Valores actuales de las estrategias con acuerdo cliente I y proveedor
|
P |
C I |
|||
|
Cumple |
No cumple |
|||
|
Cumple |
$8.060.000,00 |
$ 3.804.000,00 |
$9.850.775,00 |
$-13.314.000,00 |
|
No cumple |
$-4.984.825,00 |
$1.521.600,00 |
$340.775,00 |
$-5.325.600,00 |
Fuente: elaboración propia
El equilibrio de Nash y estrategia dominante se define en el cumplimiento del acuerdo, incentivado por la activación de multas frente al incumplimiento. Incluso, en el cuadrante No cumple (P); No cumple (CI); el flujo del proveedor es positivo, producto del valor de la opción de intercambio. En este caso, seleccionado por el proveedor el cliente II sobre I. Para el cliente I, dicho escenario no constituye una situación deseable. Cumplir para el proveedor arroja un resultado de $ 9.850.775, lo cual es preferible a no cumplir y ejercer la opción de intercambio, cuyo resultado es de $340.775. Inclusive, en la situación de incumplimiento recíproco se anulan las multas de las partes, pero el flujo a favor del cliente I es desfavorable. Conclusión: la existencia de multas cuantificadas a partir del conjunto de acciones que recíprocamente puede emprender los agentes (ecuaciones 8 y 9) incentivan el cumplimiento del acuerdo.
4.2.2 Cliente I: Sin acuerdo formal
Tabla 19: Expresiones relacionadas con las estrategias sin acuerdo cliente I y proveedor
|
P |
C I |
|||
|
Acuerdo |
No cumple |
|||
|
Acuerdo |
V=VAN(P) c/a |
V=VAN(CI) c/a |
V=-VA (P)c/a |
V=VAN(CI)s/a beneficio |
|
total |
||||
|
No cumple |
V=VAN(P)s/a beneficio |
V=-VA(CI) c/a |
V=si(VOI(II/I>0;VOII(II),VO(I)) |
V=si(VOI(II/I>0; -(VA(I) s/a); |
|
total |
VA(I) s/a |
|||
Fuente: elaboración propia
Tabla 20: Valores actuales de las estrategias sin acuerdo cliente I y proveedor
|
P |
C I |
|||
|
Acuerdo |
No cumple |
|||
|
Acuerdo |
$8.060.000,00 |
$ 3.804.000,00 |
$-1.403.000,00 |
$ 6.657.000,00 |
|
No cumple |
$9.201.200,00 |
$-3.804.000,00 |
$ 4.216.375,00 |
$-5.325.600,00 |
Fuente: elaboración propia
El equilibrio se da en el escenario no cumplir (equilibrio de pánico). No obstante, respecto del cliente I existe el incentivo a respetar el contrato. Esto es así debido a la flexibilidad estratégica que tiene el proveedor, de acuerdo con el cliente II (opción de intercambio). Sin compromiso formal ni penalidades, de mantenerse el precio de transferencia y apropiación de beneficios constantes, el proveedor tiene incentivos de no acuerdo con I ejerciendo la opción de intercambio, y consecuentemente acordar con II, con un flujo de $4.216.375. Esto origina una pérdida en I por la no provisión del servicio de -$5.325.600. El acuerdo precario arroja un flujo $8.060.000; $3.804.000 respectivamente. Es un equilibrio débil ante la ausencia de penalidades. El no cumplimiento representa un equilibrio de pánico.
4.2.3 Cliente II: Acuerdo formal con multa
Tabla 21: Expresiones relacionadas con las estrategias con acuerdo cliente II y proveedor
|
P |
C II |
|||
|
Cumple |
No cumple |
|||
|
Cumple |
V=VAN(P)c/a |
V=VAN(CII)c/a |
V=VA (indeminzación) + |
V=VAN(penalidad) CI- |
|
VOI (CII) sin acuerdo=∆(VI-VII) |
VAN(CII)s/a |
|||
|
No cumple |
V=VAN(penalidad) P- |
V=VA (indeminzación)- |
V=si(VOI(II/I>0;VOII(II),VO(I)) |
V=si(VOI(II/I>0; (VA(II) s/a-c/a) |
|
VOI (CI) sin acuerdo=∆(VI-VII) |
VAN(CII)c/a |
;-VA(II)s/a |
||
Fuente: elaboración propia
Tabla 22: Valores actuales de las estrategias con acuerdo cliente II y proveedor
|
P |
C II |
|||
|
Cumple |
No cumple |
|||
|
Cumple |
$ 10.437.500,00 |
$ 8.717.500,00 |
$ 8.931.475,00 |
$ -554.750,00 |
|
No cumple |
$ -9.502.075,00 |
$ 443.800,00 |
$ -340.775,00 |
$-895.250,00 |
Fuente: elaboración propia
Igual que aconteció con el cliente I el equilibrio de Nash y estrategia dominante se encuentra dado por el cumplimiento del acuerdo, incentivado por la activación de multas frente a la conducta maliciosa.
4.2.4 Cliente II: Sin acuerdo formal
Tabla 23: Expresiones relacionadas con las estrategias sin acuerdo cliente II y proveedor
|
P |
C II |
|||
|
Acuerdo |
No cumple |
|||
|
Acuerdo |
V=VAN(P) c/a |
V=VAN(CI) c/a |
V=-VA (P)c/a |
V=VAN(CI)s/a beneficio |
|
total |
||||
|
No cumple |
V=VAN(P)s/a beneficio |
V=-VA(CI) c/a |
V=si(VOI(II/I>0;VOII(II),VO(I)) |
V=si(VOI(II/I>0; VA(II) s/a; |
|
total |
;-VA(I)s/a |
|||
Fuente: elaboración propia
Tabla 24: Valores actuales de las estrategias sin acuerdo cliente II y proveedor
|
P |
C II |
|||
|
Acuerdo |
No cumple |
|||
|
Acuerdo |
$ 10.437.500,00 |
$ 8.717.500,00 |
$ -10.437.500,00 |
$ 4.121.000,00 |
|
No cumple |
$ 8.852.500,00 |
$ -8.717.500,00 |
$ 4.216.375,00 |
$ 7.822.250,00 |
Fuente: elaboración propia
El equilibrio débil se encuentra en la situación de acuerdo ($10.437.500; $8.717.500). Al no existir incentivos impulsados por penalidades económicas; y la incertidumbre en relación a la conducta de la contraparte, el equilibrio de no acuerdo se presenta como dominante. Esto sumado a la situación de ejercicio favorable de la opción de intercambio. En este caso el cliente II no verá vulnerada la prestación del servicio. Esto es así, en tanto y en cuanto, las variables cantidades proyectadas, precio de transferencia, probabilidades de contratación y porcentajes de apropiación de flujos se mantengan constantes.
Ilustración 1: Resolución extensiva proveedor – cliente con acuerdo formal
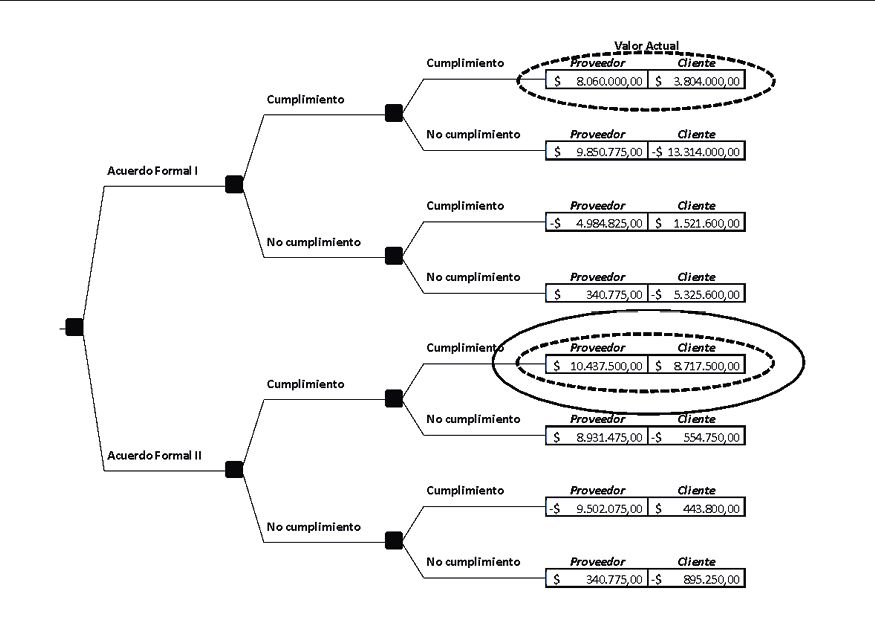
Fuente: elaboración propia
Se presenta el desarrollo extensivo correspondientes a los escenarios con acuerdo formal y sin acuerdo formal. En el primer caso, las estrategias dominantes implican el acuerdo formal con penalidades que inducen la conducta de las partes al cumplimiento. El óvalo punteado representa el equilibrio para cada cliente, la línea continua indica la solución de equilibrio para el proveedor, incentivando a un acuerdo con el cliente II.
La siguiente ilustración expone el desarrollo extensivo sin acuerdo formal. Con línea punteada se presenta el equilibrio fuerte “panic equilibrium” correspondiente al cliente I. En relación al cliente II el óvalo punteado presenta el equilibrio débil de acuerdo no formal. La línea continua expone el equilibrio fuerte para el cliente II, como la elección del proveedor de contratar con este. Dicha situación encuentra su fundamento en el resultado de la opción de intercambio. En el caso del proveedor, siendo mutuamente excluyente la elección del contratante, se inclinará por suscribir un acuerdo con el cliente II. Esto es, producto del mayor valor actual derivado de acordar con el mismo (V(CII) $10.437.500 > VA(CI) $8.060.000).
Conclusión: La estrategia a la cual se ve obligado el cliente I es la firmar de un acuerdo formal, que asegure el no ejercicio de la opción de intercambio. Dicho acuerdo evita el costo transaccional de la incertidumbre del sistema para el cliente (prestación del servicio) y protección contra la alta barrera de salida a favor del proveedor (especificidad de la inversión). Caso contrario, el proveedor debe impulsar un acuerdo con el Cliente II, quedando expuesto a condiciones menos favorables de precio. Sin acuerdo formal, el Cliente II constituye la mejor opción de negocio para el proveedor, dado la opción de intercambio. De esta manera, a través de un modelo numérico basado en el enfoque de SROG, se cuantificaron y seleccionaron estrategias y penalidades en la relación económica analizada.
Ilustración 2: Resolución extensiva proveedor – cliente sin acuerdo formal
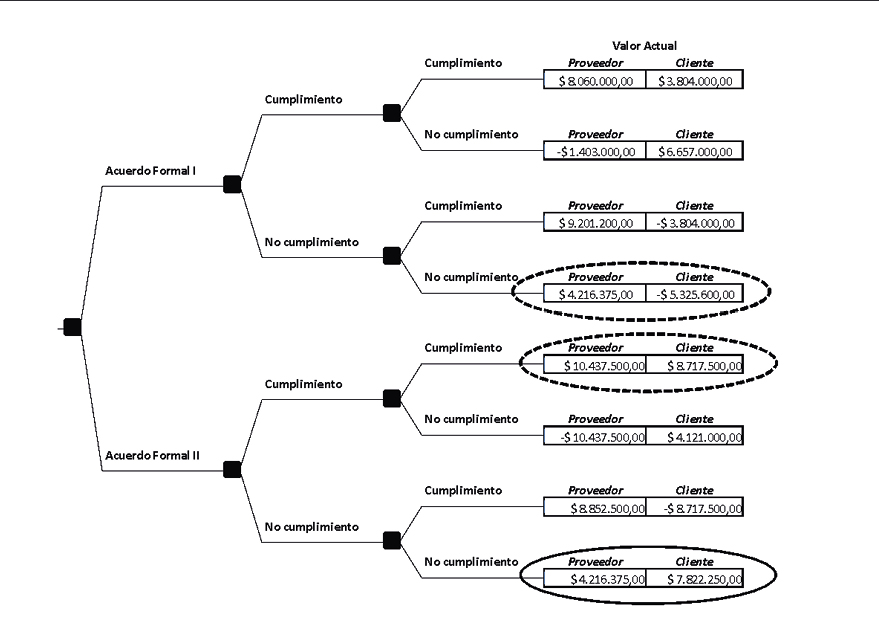
Fuente: elaboración propia
5. Conclusiones
Las estrategias, derivadas de decisiones económico financiera se encuentra sujetas a tres fuentes de riesgo: factores exógenos resumidos en el componente estado de la naturaleza, las decisiones adoptadas por el agente (empresa) y la conducta e interacción de terceros (competidores). La valoración estratégica de las relaciones económicas jurídicas queda comprendida en las fuentes de riesgos indicadas. Los modelos utilizados deben arrojar conclusiones de valor a partir de la valuación de las corrientes estocásticas de beneficios (estados de la naturaleza), flexibilidad estratégica acorde a la estructura de mercado (decisiones de la empresa) y potenciales conductas de los agentes (competidores). La literatura financiera especialidad propone modelos basados en Opciones Reales y Teoría de Juegos. Estos incorporan factores intrínsecos y exógenos derivados de las fuentes de incertidumbre a la que se exponen las partes. En base a grupo de modelos simples de opciones reales y teoría de juegos (SROG), el trabajo desarrolla una alternativa para valorar decisiones estratégicas de inversión en equipo de alta especialización para la prestación de servicios específicos. El alto grado de especialización de la inversión implica desventajas competitivas dadas las altas barreras de salida y poca reversión (nulo o bajo valor de la opción de abandono). En términos de la teoría de costos de transacción esta situación se traduce en especificidad de las transacciones.
El aporte o alcances del modelo propuesto consiste en su capacidad para valuar la corriente de beneficios esperadas por el proveedor y cliente en escenarios de acuerdo formal o, eventualmente, colaboración informal. Recrea los procesos de negociación del precio y apropiación de márgenes de ganancia, en particular frente a situaciones de compromiso informal de colaboración o simple prestación del servicio. En este escenario y desde la perspectiva de análisis del proveedor, incorpora el valor estratégico derivado de la opción de intercambio de clientes. En el caso de acuerdos colaborativos formales, su complimiento reside en los incentivos económicos para las partes bajo la forma de penalidades económicas. El trabajo aporta un modelo numérico para la estimación de las sanciones frente al incumplimiento para proveedor y cliente. El valor de las multas sigue la lógica de máximo valor entre el beneficio obtenido derivado del incumplimiento y el perjuicio generado a la contraparte, calculados con un enfoque de opciones reales y teoría de juegos.
Para el caso analizado y atendiendo a las características de los agentes, contratos de prestación de servicios, precios y poder de negociación, la estrategia dominante y equilibrio de Nash es el acuerdo con penalidades. El acuerdo colaborativo formal mitiga la exposición a riesgo, altos costos transaccionales derivados de la especificidad de la inversión (proveedor), aprovisionamiento y estabilidad de precios (clientes). Sin formalización del acuerdo, existe un equilibrio de pánico, donde las partes tiende al incumplimiento. En el caso analizado, implica para el proveedor, la prestación sin acuerdo de precios con el cliente II. Esto es así, puesto que el modelo planteado presenta la capacidad de calcular el valor estratégico de la opción de intercambio que posee el proveedor, en el marco de la Teoría de Juegos y Opciones Reales.
Las limitaciones del modelo están dadas por sintetizar el riesgo de las partes en una sola variable de estado (volatilidad). En los modelos de opciones esta resume el riesgo de mercado y tecnológico. Asimismo, parte del supuesto de que los agentes poseen información perfecta respecto de las decisiones de la contraparte. En futuras investigaciones se propone mejorar el modelo desagregando las fuentes de incertidumbre correspondientes a pagos contingentes, aplicando dos variables de estados con opciones arco iris (multinomial). Otro desafío consiste en desarrollar un modelo donde el juego de negociación de precios se plante en varias etapas, con el modelado de la conducta de inversores en juegos repetitivos, incorporando información imperfecta. En esta ocasión se pretende plantear un modelo que guie la decisión del proveedor, su exposición al riesgo de irreversibilidad, y como cuantificar las penalidades económicas que actúan como reaseguro del contrato.
REFERENCIAS
y (1999). Contractual commitments, bargaining power and governance inseparability: Incorporating history into transaction cost theory. Academy of Management Review, 24 (1), pp. 49-63. doi.org/10.2307/259036
y (2000). The role of prior commitment in governance choice. En: N. V. Foss, ed. Competence, governance and entrepreneurship. Oxford: Oxford University Press, pp. 223-249. doi:10.1093/oso/9780198297178.003.0011
, y (2009). Optimal investment decisions for two positioned firms competing in a duopoly market with hidden competitors. European Financial Management, 17, 305-330. doi: 10.1111/j.1468-036X.2009.00514.x
(1986). La Evolución de la Cooperación. Madrid, España: Alianza Editoria S.A.
, y (2014). Developing real option game models. European Journal of Operational Research, 237(3), 909-920, doi. org/10.1016/j.ejor.2014.02.002
y (2000). Multiple considerations in making governance choices: Implications of transaction cost of economics, real option theory and knowledge-based theory of the firms. En: Competence, Governance and Entrepreneurship. Oxford University Press, pp. 232-249.
, y (2012). A dynamic duopoy investement game without commitment under uncertainty market expansion. Interntational Journal of Industrial Organization, 30, 663-681. doi.org/10.1016/j.ijindorg.2012.07.005
, y (2005). Using binomial decision trees to solve real options-valuation problems. Journal of Decision Analysis (2), 2 642-648 doi.org 10.1287/deca.1050.0040
, y (2012). Volatility estimation for stochastic project value models. European Journal of Operational Research, (220), 3 642-648 doi.org /10.1016/j.ejor.2012.01.059
(2010). El estudio de casos como metodología de investigación y su importancia en la dirección y administración de empresas. Revista Nacional de Administración, 2(1), 31-54. doi:10.22458/rna.v1i2.332
(2008). A Synthesis of Binomial Option Pricing Models for Lognormally Distributed Assets. Journal of Applied Finance, (18), 1, SSRN: https://ssrn.com/abstract=2698699
y (2013). Strategic Management and Competitive Advantage. Competitive Strategy, 47-74, doi.10.7551/mitpress/9780262015998.003.0002
y (2001) Real Options: A practitioner guide´s. New York Texere Publishing Limited.
, y (1979). Option Pricing: A Simplified Approach. Journal of Financial Economics, 7(3), 229-263. doi:10.1016/0304-405X(79)90015-1
y (1994). Investment under Uncertainty (1 ed.). New Jersey: Pricenton University Press.
, , y (2022). Demand uncertainty, product differentiation, and entry timing under spatial competition. European Journal of Operational Research, 303(1), 286-297, doi. 10.1016/j.ejor.2022.02.041
y (1985). Preemption and rent equalization in the adoption of new technology. Review of Economics Studies, 52(3), 383-401. doi.org/10.2307/2297660
y (1985). Exit. Journals of Economics, 16(2), 184-194. RePEc:rje:randje:v:16:y:1985:i:summer:p:184-194
(2018). Actualidad de los agentes de sostén. Petrotecnia, 26-35. Recuperado el 15 de marzo de 2021, de http://www.petrotecnia.com.ar/Petro_1_18/Actualidad.pdf
(2006). Monte Carlo estimation of project volatility for real options analysis. En estudos do GEMF (grupo de estudios monetarios y financieros) Universidad de Coimbra, de https://www.researchgate.net/publication/5081218_Monte_Carlo_Estimation_of_Project_Volatility_for_Real_Options_Analysis.
(2015). Estimating state-dependent volatility of investment projects: a simulation approach, En estudos do GEMF (grupo de estudios monetarios y financieros) Universidad de Coimbra de https://repec.uc.pt/gmf/wpaper/wpgemf/gemf_2015-02.pdf
(2011). Strategic real options under asymmetric information. Journal of Economics and Dynamic Control, 35(6), 922-934. doi.org/10.1016/j.jedc.2011.01.001
(1996). The strategic exercise of options: Development cascades and overbuilding in real state markets. Journal of Finance, 51(5), 1653-1679. RePEc:bla:jfinan:v:51:y:1996:i:5:p:1653-79
(2000). Options exercise games: The intersection of real options and game theory. Journal of Applied Corporate Finance, 13(2), 99-107. doi.org/10.1111/j.1745-6622.2000.tb00057.x
(2002). Option exercise games: an application to the equilibrium investment strategies of firms. Review of Financial Studies, 15(3), 691-721. doi.org/10.1093/rfs/15.3.691
(2009). Game Theory Evolving (2 ed.). United Kingdom: Princeton University Press.
y (1995). Performance implications of buyer-suppler relationship in industrial markets: a Transaction Cost Explanation. Journal of Business Research, 32, pp. 57-66. doi.org/10.1016/0148-2963(94)00010-C
y (2007). Pre-emptive patenting under uncertainty and asymmetric information. Annals of Operations Research, 151, 5-28. doi: 10.1007/s10479-006-0125-5
, y (1978). Vertical integration, appropiate rents and competitive contracting process. Law Economics, 21, pp. 297-326. DOI: 10.1086/466922
(1982). Rational Cooperation in Finitely Repeated Prisioners´ Dilemmas. Journal of Economics Theory, 27, 245-252. doi.org/10.1016/0022-0531(82)90029-1
y (1998). Strategic growth options. Management Science, 44(8), 1021-1031. doi.org/10.1287/mnsc.44.8.1021
(2001). The impact of debt financing on entry and exit in duolpoly. Review of Financial Studies, 14(3), 765-804. RePEc:oup:rfinst:v:14:y:2001:i:3:p:765-804
(2023a). Opciones Reales Multinomiales con dos variables de estado y Teoría de juegos en la valoración de estrategias de inversión. Revista mexicana de economía y finanzas, 18(4). https://doi.org/10.21919/remef.v18i4.903
(2023b). Valoración de estrategias competitivas, acuerdos colaborativos y penalizaciones con Opciones Reales Multinomiales y Teoría de Juegos. Revista de métodos cuantitativos para la economía y la empresa, 35, pp. 26-41 https://doi.org/10.46661/revmetodoscuanteconempresa.6092.
y (2015). Un modelo consolidado de opciones reales, teoría de juegos y análisis de costos de transacción para el diseño de acuerdos contractuales. Revista de Economía Política de Buenos Aires, 14, 59-81.
(2004). Exit in duopoly under uncertainty. Journal of Economics, 35(1), 111-127, doi.org /10.2307/1593732
(1953). Two-Person Cooperative Games. Econometrica, 21(1), 128-140. RePEc:rje:randje:v:35:y:2004:1:p:111-127
, y (2019). Volatilidad en opciones reales: revisión literaria y un caso de aplicación en el sector petrolero colombiano. Revista de Métodos Cuantitativos para la Economía y la Empresa (27), 1 135-155 RePEc:pab:rmcpee:v:27:y:2019:i:1:p:136-155
y (2006). Real options in an asymmetric duopoly: Who benefits from your competitive disadvantage? Journal of Economics and Management Strategy, 15(1), 1-35. doi.org/10.1111/j.1530-9134.2006.00090.x
y (2003). Rivalry under price and quantity uncertainty. Review of Financial Economics, 14, 209-224. doi.org/10.1016/j.rfe.2005.04.002
(2014). Arenas más allá del acatamiento de las normas. Petrotecnia, 66-81. Recuperado el 08 de marzo de 2021, de http://www.petrotecnia.com.ar/junio14/Petro/Arenas.pdf
y (2004). Managing commitments and flexibility by real options. Industrial Marketing Management, 33, pp. 501-512. doi.org/10.1016/j.indmarman.2004.03.003
(2003). Infrastructure investment as a real options game: The case of European airport expansion. Financial Management, 32(4), 5-35. doi: 10.2139/ssrn.423500
y (1993). A real options and game-theoretic approach to corporate investment strategy under competition. Financial Management, 22(3), 241-250. doi:10.2307/3665941
y (2004). Strategic Investment: Real Options and Games (1 ed.). New Jersey, Estados Unidos: Princeton University Press.
(2010). Preemption in a real option game with a first mover advantage and a player-specific uncertainty. Journal of Economics Theory, 145, 2448-2462. doi.org/10.1016/j.jet.2010.10.002
, 1983. Credible commitments: Using hostages to support exchanges. American Economics Review, 73(4), pp. 519-540. RePEc:aea:aecrev:v:73:y:1983:i:4:p:519-40
, 1985. The economics institutions of capitalims. New York: The Free Press.
, , y (2024). Strategic investment under uncertainty: why multi-option firms lose the preemption run. Journal of the Operational Research Society, 75(9), 1855-1872, doi. 10.1080/01605682.2023.2281535
(2020). Opciones reales: una guía teórico-práctica para la valoración de inversiones bajo incertidumbre mediante modelos en tiempo discreto y simulación de Monte Carlo. Universidad Externado de Colombia