6431_RefCru

En este artículo, se evalúa el riesgo de mercado asociado a los mercados financieros de New York y Colombia en tres períodos pertenecientes a la ventana temporal 2019-2020, caracterizados por condiciones económicas y sociales impactantes como la guerra de precios del petróleo entre Arabia Saudita y Rusia y la pandemia mundial por COVID-19. Se realiza la medición de riesgo por medio del uso del valor en riesgo (VaR) y déficit medio (MS), aplicando una metodología estadística que considera el uso de técnicas de remuestreo (Bootstrapping) paramétrico y no paramétrico. Se tomaron datos de cinco índices (Standard and Poor’s 500, Dow Jones, COLCAP, VIX y Brent) con el fin de evaluar los efectos ocasionados por variables como el precio del petróleo y las condiciones generadas por la pandemia COVID-19 en las fechas de estudio, como resultado principal se obtiene que en general se presenta una volatilidad muy elevada en los periodos afectados por los dos fenómenos ya mencionados cuando se dieron de manera simultánea, y que además de grandes caídas en los índices de referencia, también se tiene la evidencia de grandes recuperaciones que contribuyen positivamente a la tendencia en los precios.

PALABRAS CLAVE

Riesgo de mercado; Volatilidad; Valor en riesgo; Déficit Medio; Crisis; COVID-19; Mercados financieros.

ABSTRACT

In this article, the market risk associated with the financial markets of New York and Colombia is evaluated in three periods belonging to the 2019–2020-time window, characterized by shocking economic and social conditions such as the oil price war between Saudi Arabia and Russia and the global pandemic by COVID-19. Risk measurement is carried out using the value at risk (VaR) and Median Shortfall (MS), applying a statistical methodology that considers the use of parametric and non-parametric resampling techniques (Bootstrapping). Data from five indices (Standard and Poor’s 500, Dow Jones, COLCAP, VIX and Brent) were taken in order to evaluate the effects caused by variables such as the price of oil and the conditions generated by the COVID-19 pandemic on the dates of study, as the main result it is obtained that in general there is a very high volatility in the periods affected by the two aforementioned phenomena when they occurred simultaneously, and that in addition to large falls in the reference indices, there is also evidence of large recoveries that contribute positively to the trend in prices.

KEYWORDS

Market risk; Volatility; Value at risk; Median Shortfall; Crisis; COVID-19; Financial markets.

Clasificación JEL: G11, G15, G24

MSC2010: 62M10, 62P20, 91G10, 91G70, 91G80

1. INTRODUCCIÓN

Los índices bursátiles se sugieren como buenos indicadores de la situación económica de un país, analizar su comportamiento permite establecer un diagnóstico sobre la percepción del riesgo y el optimismo sobre los mercados financieros. El 30 de enero de 2020, la Organización Mundial de la Salud (OMS) declaró que el brote en china del virus COVID-19 era una emergencia de salud pública de preocupación internacional que presentaba un alto riesgo para los países con sistemas de salud vulnerables (World Health Organization. Coronavirus disease 2019 (COVID-19) Situation Report-43, 3 de marzo de 2020). El 11 de marzo de 2020 se declara como pandemia, con ello los principales índices bursátiles del mundo experimentaron caídas como es el caso del Promedio Industrial Dow Jones con una caída del 18 % referente al 30 de enero de 2020, un 17 % para el índice Standard and Poor’s 500 y el 13 % (en comparación con el 17 de enero del mismo año) para el índice Hang Seng de China. La pandemia por COVID-19 no tiene comparación con algún evento similar en tiempos contemporáneos, tomando como ejemplo la epidemia del Sars en el 2003, el índice Msci Pacific de Japón a pesar de sus caídas en marzo, obtuvo un rendimiento de 42.5 % para todo el año, por otro lado, la crisis del año 2008 inicia en Estados Unidos y se extiende gradualmente en el mundo, mientras el impacto del COVID-19 fue casi instantáneo y universal (Ozkan, 2021). En resumen, su impacto, repercusiones y características unidas son únicas.

Mientras se desarrollaban medidas para la contención de la pandemia, las tensiones entre los dos miembros más importantes de la OPEP (Organización de Países Exportadores de Petróleo), Rusia y Arabia Saudita, trajeron aumentos en la oferta del crudo, la demanda se había disminuido debido a la parada en la producción industrial de diversos países, lo que conllevó a que los precios del barril de referencia Brent llegaran más allá de mínimos no vistos desde el año 2002 y la referencia WTI se situase en valores negativos (Bourghelle et al., 2021). Al ser el petróleo el principal recurso en países industrializados, los cambios en los precios generan un gran impacto en los mercados bursátiles internacionales (Wei et al., 2019), a tal punto que se ha llegado a interpretar, que el aumento en los precios del crudo conduce a contracciones en el crecimiento económico debido al aumento de los costos de producción de las compañías asociadas con el crudo (Sarwar et al., 2019).

Según Lorenzo Valdés (2016), la incertidumbre que se le atribuye a los momentos de crisis aumenta el sesgo cognitivo referente a la valoración de los activos de mercado (Lorenzo, 2016) y los inversores mejor informados son los que aprovechan dichas condiciones, es así como las acciones de estos son determinantes de la volatilidad de algún activo. Respecto al riesgo de mercado, siempre está presente y el inversor considera a priori que la probabilidad de eventos extremos es baja, sin embargo, en momentos de crisis la volatilidad del mercado se torna inesperada, como se evidenció en la gran depresión de 1929 y en la crisis hipotecaria del año 2008, momentos en los que criterios como Valor en Riesgo (VaR) fueron importantes para entender el comportamiento de los cambios en la economía.

De acuerdo con la revisión de la literatura, se han desarrollado diversas estrategias para el cálculo del VaR y el CVaR (Valor en Riesgo Condicional), sin embargo y en general los autores suelen clasificarlas de acuerdo con el supuesto considerado para explicar teóricamente el comportamiento del índice, al asumir el mismo como una variable aleatoria, de modo que, desde la estadística, se tienen estrategias que consideran métodos paramétricos, no paramétricos y semiparamétricos (Xu et al., 2021). El cálculo del VaR por el tradicional método de usar los cuantiles de la serie de valores históricos de los rendimientos, por ejemplo, tiene características a favor y en contra, puesto que en periodos de tranquilidad funciona bien, mientras en periodos inestables se tiende a subestimar el riesgo (Li, 2017), razón por la cual se ha intentado desarrollar metodologías que permitan mayor efectividad del método de cálculo del indicador y que posean una mayor aplicabilidad. Algunas metodologías tienen en cuenta datos intradía como el rango, soportándose en la relevancia de la volatilidad en periodos de tiempo menores a un día (Meng & Taylor, 2018), otras como las aplicadas por Ardia & Hoogerheide (2014); So & Yu (2006) han abordado el tema usando modelos de series de tiempo tipo GARCH y FIGARCH, con los que se pretende captar la característica variable en el tiempo de la volatilidad del mercado, teniendo en cuenta la ponderación de los rendimientos históricos.

Algunos estudios como los de Hoogerheide, Lennart F. han discutido la importancia de la frecuencia de estimación del VaR y su relevancia en el nivel de certeza (Ardia & Hoogerheide, 2014), es inteligible que el cambio en las ventanas de tiempo de estimación produzcan diferencias en el cálculo del índice y que medidas complementarias sean requeridas para valorar el riesgo, de tal modo ya en tiempos recientes se ha dado una mayor atención al análisis del CVaR, asegurando que este último tiene propiedades sub aditivas, característica que en general no posee el VaR (Kim & Kang, 2021). Con el CVaR es posible incluso estimar una medida coherente que permita analizar el valor de un activo considerando las pérdidas aleatorias de otro riesgo asociado (Josaphat & Syuhada, 2021). A pesar de la amplia acogida de las medidas ya mencionadas, aún existe debate sobre su pertinencia y aplicabilidad, surgiendo así medidas alternativas como el MS (por sus siglas en inglés Median Shortfall), definida como la mediana de las pérdidas ocurridas más allá del VaR (Kou & Heyde, 2013), que propone un enfoque alternativo a las medidas ya conocidas. Finalmente, el objetivo preponderante en el estudio del riesgo es la búsqueda de herramientas que conduzcan a una mejor cuantificación del riesgo mismo y por ende a tomar las mejores decisiones que lo minimicen.

En este artículo se aplica una metodología estadística para estudiar el comportamiento de las medidas VaR y MS en cinco índices financieros, uno de Colombia, tres de Estados Unidos y la referencia Brent durante períodos del año 2020 en los que la economía mundial se vio afectada por fenómenos como la guerra de precios del petróleo, la pandemia por COVID-19 y la interacción de ambos eventos. Se compara el comportamiento de los indicadores con períodos de tiempo similares en el año inmediatamente anterior (2019). La evaluación se realiza utilizando como variable aleatoria los rendimientos logarítmicos de los retornos. Dividir el archivo de datos en períodos cortos disminuye de manera importante los tamaños de las series de observaciones usadas para la estimación de los indicadores de riesgo, lo cual motivó el hecho de hacer uso de metodologías basadas en Bootstrapping tanto paramétrico como no paramétrico para el cálculo del riesgo.

La estructura del trabajo es la siguiente: en la sección 2 describimos la metodología utilizada dividida en dos etapas; en la sección 2.1, definimos la muestra y los datos y realizamos análisis exploratorio; en la sección 2.2 se expone la propuesta para calcular la medición de riesgo y los métodos estadísticos aplicados; en la sección 3, presentamos los principales resultados, finalmente en la sección 4 se enuncian las conclusiones relevantes.

2. Metodología

El desarrollo metodológico se estableció en dos etapas:

Etapa 1. Adecuación de los archivos de datos obtenidos a través de las páginas web (Google Finance, 2021; Investing, 2021) y análisis estadístico exploratorio de los rendimientos calculados.

Etapa 2. Propuesta metodológica de procedimientos para calcular el VaR y el CVaR-MS usando métodos estadísticos soportados en distribuciones de probabilidad y métodos no paramétricos.

Gráfica 1

Gráfica 1. Metodología por etapas

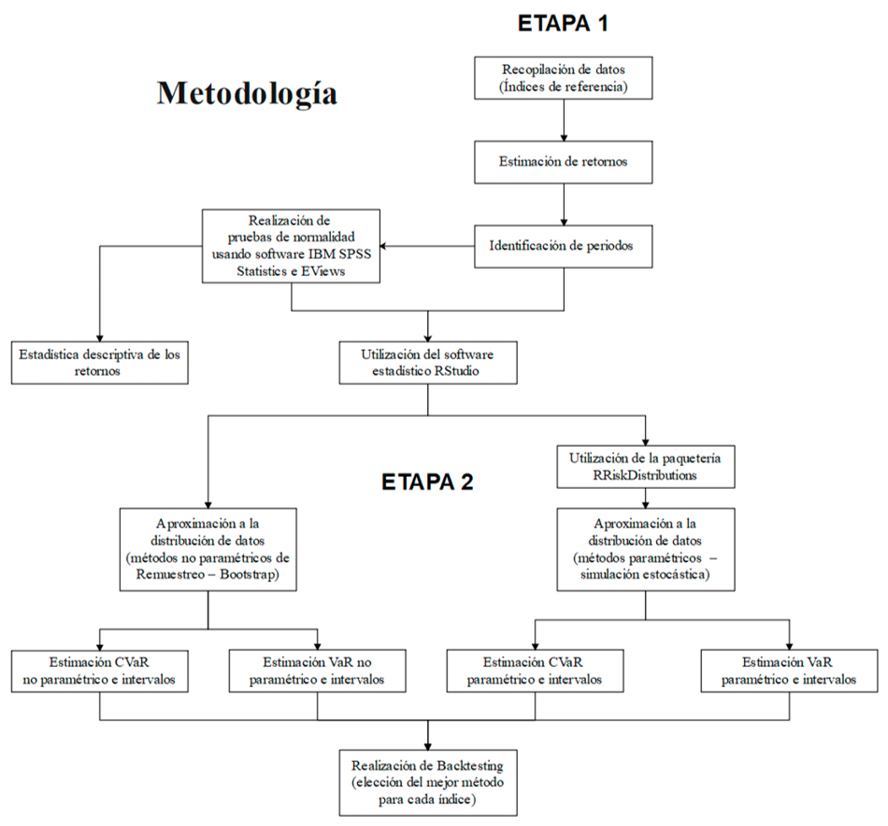
Fuente: Elaboración propia

2.1 Etapa 1. Adecuación de los archivos de datos obtenidos a través de las páginas web (Google Finance, 2021; Investing, 2021) y análisis estadístico exploratorio de los rendimientos calculados

Se tomaron los valores diarios en dólares del índice bursátil Standard and Poor’s 500 (SP), índice que incluye 500 empresas estadounidenses líderes que cotizan en bolsa, elegidas por algunos criterios como liquidez, volumen de acciones negociadas en bolsa y capital flotante; el índice industrial Dow Jones (DJ), el cual realiza un seguimiento de 30 grandes empresas, las más representativas que cotizan en la Bolsa de Valores de Nueva York (NYSE) y Nasdaq; el índice de volatilidad (VIX) (Google Finance, 2021); el índice del mercado de valores de Colombia (COLCAP) (el índice COLCAP reemplazó al IGBC como el principal indicador del comportamiento del mercado accionario colombiano a partir del 1 de noviembre de 2013), el cual refleja las variaciones de los precios de las 20 acciones más líquidas de la Bolsa de Valores de Colombia (BVC), país considerado como una de las economías emergentes de mayor proyección de acuerdo a “The Report: Colombia 2013” (Oxford Business Group, 2013), por último se tuvo en cuenta la cotización del precio del petróleo (Brent) (Investing, 2021) y a todos se les calculó el retorno logarítmico. Con el fin de evaluar las distintas condiciones económicas globales y sus efectos sobre los índices analizados, se procedió a dividir la información de acuerdo con los periodos de tiempo que aparecen en la tabla 1.

Tabla 1

Tabla 1. Períodos de tiempo establecidos para el estudio del efecto de las condiciones de la economía mundial sobre el comportamiento de cinco índices de referencia

Periodo	Fechas	Descripción	Cantidad de datos
2019	30 de enero al 30 de agosto de 2019	Periodo de comparación para el periodo 2020	141
1	30 de enero al 5 de marzo de 2019	Periodo de comparación para el periodo cuatro	24
2	6 de marzo al 22 de abril de 2019	Periodo de comparación para el periodo cinco	31
3	23 de abril al 30 de agosto de 2019	Periodo de comparación para el periodo seis	86
2020	30 de enero al 30 de agosto de 2020	COVID como preocupación internacional hasta fin de cuarentena en Colombia	140
4	30 de enero al 5 de marzo de 2020	COVID antes de guerra. Se toma como referencia la declaración de la OMS: COVID como preocupación internacional	25
5	6 de marzo al 21 de abril de 2020	COVID y guerra. Se toma como referencia la reunión de la OPEP en Viena y el anuncio de NO ACUERDO por parte de Rusia hasta la fecha que registra el peor cierre del precio del petróleo	30
6	22 de abril al 31 de agosto de 2020	COVID y posguerra. Día siguiente al peor cierre del precio del petróleo hasta fin de fase de cuarentena estricta en Colombia	85
7	1 de septiembre al 30 de diciembre de 2020	COVID y posguerra sin cuarentena estricta. Día después del fin de cuarentena estricta hasta finalización de año 2020	80

Fuente: Elaboración propia

En la construcción de las series de datos, se contempló tomar solo los valores de los días en los que todos los índices son calculados, es decir, no se consideraron los fines de semana y los días festivos. Se obtuvieron los rendimientos logarítmicos y se aplicaron pruebas estadísticas Kolmogorov-Smirnov, Shapiro-Wilk y Jarque-Bera para evaluar el ajuste de los datos a diferentes distribuciones de probabilidad incluido el modelo normal que es el de mayor uso en los estudios revisados. Las pruebas de bondad de ajuste se realizaron con la ayuda de los programas estadísticos SPSS, EViews y la librería “Rriskdistributions” del software estadístico R, partiendo del supuesto de que el comportamiento natural de la variable permanece constante en el período de tiempo que está siendo afectado por algún proceso externo que altera las condiciones de la economía. Para todos los casos, se asumió como máximo error tipo I, un valor de 0.05. Las pruebas estadísticas permitieron concluir que el modelo Cauchy podría ser un buen candidato para ajustar las distribuciones de los indicadores en el año 2020.

2.2 Análisis exploratorio

Tabla 2

Tabla 2. Estadísticas descriptivas de los Rendimientos

	SP2019	SP2020	SP1	SP2	SP3	SP4	SP5	SP6
Media	0.0007	0.0005	0.0023	0.0014	0.0000	–0.0033	–0.0028	0.0028
Mediana	0.0010	0.0030	0.0010	0.0010	0.0010	–0.0020	–0.0060	0.0040
Desv. est.	0.0084	0.0276	0.0058	0.0066	0.0095	0.0212	0.0525	0.0128
Mínimo	–0.0300	–0.1280	–0.0090	–0.0190	–0.0300	–0.0450	–0.1280	–0.0610
Máximo	0.0210	0.0900	0.0150	0.0150	0.0210	0.0450	0.0900	0.0310
	DJ2019	DJ2020	DJ1	DJ2	DJ3	DJ4	DJ5	DJ6
Media	0.0004	0.0000	0.0020	0.0007	–0.0002	–0.0038	–0.0035	0.0024
Mediana	0.0000	0.0015	–0.0005	0.0000	0.0005	–0.0040	–0.0055	0.0040
Desv. est.	0.0083	0.0298	0.0071	0.0062	0.0092	0.0225	0.0561	0.0148
Mínimo	–0.0310	–0.1380	–0.0090	–0.0180	–0.0310	–0.0450	–0.1380	–0.0710
Máximo	0.0200	0.1080	0.0180	0.0130	0.0200	0.0500	0.1080	0.0380
	COLCAP2019	COLCAP2020	COLCAP1	COLCAP2	COLCAP3	COLCAP4	COLCAP5	COLCAP6
Media	0.0007	–0.0022	0.0025	0.0015	–0.0002	–0.0022	–0.0105	0.0007
Mediana	0.0020	0.0000	0.0010	0.0030	0.0010	0.0000	–0.0030	0.0010
Desv. est.	0.0089	0.0286	0.0060	0.0103	0.0090	0.0100	0.0560	0.0144
Mínimo	–0.0270	–0.1330	–0.0110	–0.0220	–0.0270	–0.0230	–0.1330	–0.0490
Máximo	0.0210	0.1250	0.0120	0.0170	0.0210	0.0210	0.1250	0.0350
	VIX2019	VIX2020	VIX1	VIX2	VIX3	VIX4	VIX5	VIX6
Media	0.0008	0.0060	–0.0109	–0.0038	0.0058	0.0353	0.0083	–0.0034
Mediana	–0.0080	–0.0110	–0.0110	–0.0110	–0.0055	0.0090	–0.0150	–0.0120
Desv. est.	0.0819	0.1034	0.0499	0.0600	0.0950	0.1377	0.1362	0.0743
Mínimo	–0.1980	–0.2660	–0.0850	–0.1130	–0.1980	–0.1820	–0.2660	–0.1410
Máximo	0.3340	0.3920	0.0950	0.1900	0.3340	0.3820	0.3580	0.3920
	BRENT 2019	BRENT 2020	BRENT 1	BRENT 2	BRENT 3	BRENT 4	BRENT 5	BRENT 6
Media	0.0005	–0.0026	0.0028	0.0035	–0.0012	–0.0074	–0.0304	0.0087
Mediana	0.0020	0.0010	0.0045	0.0020	0.0010	–0.0080	–0.0375	0.0050
Desv. est.	0.0173	0.0568	0.0137	0.0092	0.0202	0.0234	0.1023	0.0339
Mínimo	–0.0740	–0.2800	–0.0360	–0.0130	–0.0740	–0.0660	–0.2800	–0.0790
Máximo	0.0460	0.1910	0.0260	0.0280	0.0460	0.0320	0.1910	0.1300

Fuente: Elaboración propia

De acuerdo con los resultados de la Tabla 2. en general para el periodo 2019 la media de los rendimientos para todos los indicadores es mayor en comparación con los mismos períodos en el año 2020. La excepción está en el VIX cuya media es 0.0008 en el año 2020 y 0.0060 en el 2019, dicho comportamiento tiene intrínseco la volatilidad del índice S&P500.

Los mínimos y máximos en los rendimientos de los indicadores de referencia fueron superados en el periodo 2020 en comparación con los registros del año 2019, es claro que dichos resultados son debido al impacto de los eventos relacionados al COVID-19 y discusiones entre miembros de la OPEP, siendo más precisamente el periodo cinco en el que se estaban presentando simultáneamente los efectos del COVID-19 y las tensiones de la OPEP, lo que caracteriza este subperiodo como el más complejo en términos financieros. Es importante hacer énfasis en los movimientos de la desviación estándar para todos los indicadores, es evidente que en el subperiodo cinco se presentó la volatilidad más importante, pues se observaron los registros más bajos y más altos de todos los indicadores a excepción del VIX, este último presentó su registro más alto en el periodo seis (comprendido entre el 22 de abril y 31 de agosto del año 2020) el cual puede ser considerado como de transición hacia la mejoría. En este subperiodo se presentó la media más alta entre los subperiodos evaluados para los retornos de los indicadores S&P500, Dow Jones y Brent, lo cual pudo deberse a la esperanza de los inversores en que los avances con las vacunas pondrían fin a la crisis.

2.3 Etapa 2. Propuesta metodológica de procedimientos para calcular el VaR y el CVaR-MS usando métodos estadísticos soportados en distribuciones de probabilidad y métodos no paramétricos

El valor en riesgo es una de las formas más aceptadas para cuantificar la volatilidad de un activo y es definido como la máxima pérdida esperada en un portafolio con cierto nivel de confianza en un determinado período de tiempo (Alonso & Chaves, 2013). El valor en riesgo condicional (CVaR) o déficit esperado (ES) como se trata más comúnmente en la actualidad (Geenens & Dunn, 2022), es una medida que por su parte intenta estimar el valor promedio que puede obtenerse entre los menores retornos posibles con un nivel de confianza (1- α), en cambio el déficit medio (MS) resulta equivalente pero con un cambio sutil respecto al ES, el MS consiste en estimar la mediana (en lugar de la media) de las pérdidas ocurridas más allá del VaR (Kou et al., 2013), siendo α una significancia estadística a considerar (máximo error tipo I que se espera tener). De esta forma las medidas de riesgo permiten a un inversionista ajustar su capital a las pérdidas menos probables, pero de mayor cuantía que puedan impactar su portafolio financiero, es decir adecuar los requisitos de capital propio, fijar límites del riesgo asumido por los operadores y funcionar como un vehículo de información para los operadores de mercado e instituciones financieras (Feria Domínguez, 2005).

Métodos paramétricos usando simulación estocástica con remuestreo (Bootstrap). La distribución normal es ampliamente conocida por su uso en el cálculo del VaR y CVaR (Ahmed et al., 2021). El uso más convencional sugiere que la probabilidad α de tener rendimientos menores a lo que es el VaR para un periodo t, se puede estimar como P (x < VaRt ) = α bajo el supuesto que, el retorno x se distribuye N(μ ,σ) y los parámetros de la distribución toman los valores de las estimaciones obtenidas a partir de los datos históricos de la serie. La primera propuesta metodológica consiste en estimar los parámetros utilizando los rendimientos diarios calculados para la serie de tiempo y generar muestras aleatorias bajo el supuesto de normalidad mediante simulación estocástica de cadenas de datos de mayor tamaño (10,000 observaciones). Para cada muestra simulada se calcula el VaR y el MS con un nivel de confianza del 95 %, el procedimiento se repite m=10,000 veces, de modo que se tienen m estimaciones de los indicadores de riesgo. La estimación final, será la media de la distribución obtenida para el indicador, la cual se acompaña de un intervalo de confianza obtenido a partir de los percentiles de la distribución empírica de las m estimaciones.

En una segunda forma de calcular los indicadores de riesgo, se asumió que los retornos pueden ser ajustados a través de una distribución Cauchy de probabilidades la cual es simétrica respecto a un valor central. La función de densidad de probabilidad de la distribución (Johnson, Kotz y Balakrishnan, 1995) aparece en la ecuación 1.

(1)

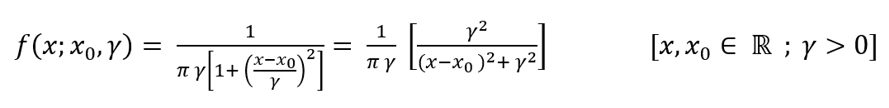
Los parámetros x0 ,y γ identifican la localización y la forma de la distribución (15) y son estimados a través de la mediana muestral (estimador para x0) y 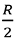como un estimador aproximado de γ siendo R el rango intercuartílico de la muestra, R = Percentil75 - Percentil25. De este modo, los parámetros calculados son usados para la generación de muestras aleatorias y posteriormente el cálculo de los indicadores de riesgo se realiza replicando el proceso usado con la distribución normal.

Propuesta de método no paramétrico usando remuestreo (Bootstrap). Las aproximaciones no paramétricas hacen uso de los datos de la serie y no asumen alguna distribución de probabilidad específica para explicar su comportamiento (Alonso & Chaves, 2013), de modo que, se pretende proyectar una posible distribución de los datos, esperando que dicha distribución sea fiel a determinado periodo histórico disponible. De acuerdo con la literatura, uno de los métodos no paramétricos más comúnmente usado para el cálculo del VaR es la simulación histórica (Alonso & Chaves, 2013). Se ordenan los rendimientos históricos (X) de menor a mayor fijándose específicamente en el percentil empírico de la distribución muestral que represente un nivel de significancia deseado (comúnmente se emplea 1 % o el 5 %) y el VaR estimado es obtenido mediante la ecuación 2.

(2)

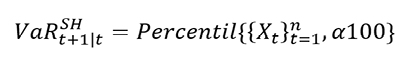
El método que se propone, utiliza el procedimiento estadístico de re muestreo (Bootstrap en inglés) el cual puede ser paramétrico o no paramétrico (Davison & Hinkley, 1997). En el primer caso, se toma la muestra original de rendimientos, se asume que los mismos pueden ser modelados con una distribución de probabilidades conocida y se estiman los parámetros utilizando los datos (Chernick, 2008; Efron, 2007). Asumiendo que los valores estimados con los datos de la muestra, son los parámetros, se simulan m muestras de la distribución con esos parámetros y del mismo tamaño n de la muestra original y para cada muestra se obtiene el indicador de interés. La estimación final se obtiene calculando la media aritmética de los indicadores calculados. El remuestreo no paramétrico, consiste en tomar la muestra original de rendimientos diarios, bajo el supuesto que la transformación permite observar datos independientes e idénticamente distribuidos y construir muestras con repetición de igual tamaño a la original (Tibshirani & Efron, 1993). De esta forma se generaron m = 10,000 muestras aleatorias con sustitución provenientes de la muestra original de tamaño nj (j identifica el período de estudio) y para cada muestra se calculó el VaR y el déficit medio (MS) con un nivel de confianza del 95 %, utilizando el procedimiento tradicional de ordenar los datos y evaluar el percentil asociado a la significancia estadística. Para el caso del VaR, se tomaron las 10,000 estimaciones obtenidas por periodo o sub periodo y se calculó la media de las mismas y su intervalo de confianza Bootstrap. Hallado el VaR para un nivel de significancia α en cada muestra se aplica la ecuación 3 para todos los valores ordenados de la submuestra desde L (el menor de los rendimientos) hasta el nivel VaR, calculando el valor MS para cada muestra.

(3)

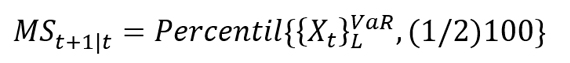
En el caso de la decisión sobre el uso típico del CVaR o su propuesta alterna MS, se diseñaron los histogramas de las colas pertenecientes a las distribuciones originales de los rendimientos, se observó la apariencia de cada distribución perteneciente a cada índice. Dado que, para la mayoría de los casos, la forma no era simétrica, se decidió tomar como aproximación del CVaR la mediana de los datos y no la media como es común, es decir el MS. Una buena justificación a dicha decisión puede hallarse en el trabajo de Erdely (2017), donde fundamenta la bondad de la mediana sobre la media exponiendo que la mediana siempre existe para variables aleatorias continuas, además de considerarse como una medida robusta, en cambio, la media podría ser numéricamente inestable bajo distribuciones de probabilidad de cola pesada o incluso no existir (Erdely, 2017). Por otro lado, autores como Rodríguez (2017) indican que las series de rendimientos bursátiles tienen una distribución de colas pesadas, por lo tanto es de esperarse mayor concentración probabilística en las colas (Rodríguez, 2017), esto sugiere como pertinente el uso de medidas estadísticas que sean coherentes y aplicables a la naturaleza de dichas distribuciones. También autores como Kou y Peng (2014) han discutido sobre la bondad del uso de la mediana en el CVaR señalando 3 factores primordiales; como primer factor enuncian la elicitabilidad como propiedad valiosa del concepto Median Shortfall que permite comparar modelos de pronóstico apuntando a minimizar el error promedio del backtesting, afirmando que el CVaR con su formulación original no la tiene; en segundo lugar se menciona la robustez distribucional con la que cuenta, atribuyéndole mayor estabilidad y menor sensibilidad a valores extremos en comparación con el uso del promedio, y por último se habla de la facilidad de aplicación o poca dificultad de implementación (Kou & Heyde, 2013).

La estimación final para el MS será entonces la media de las 10,000 medianas y los valores de los percentiles empíricos 2.5 y 97.5 el intervalo de confianza. A modo de ilustración del uso de la mediana de la cola como indicador de riesgo CVaR, se puede tomar los datos del Brent en el periodo 2019. La media de los datos menores al percentil 5 % en el periodo 2019 fue de -0.043 y la mediana fue de -0.038. Se observó que, el 1.42 % de los datos eran menores a la media, mientras que el 2.84 % de las observaciones era menor a la mediana (el doble), en otras palabras, una entidad u operador de mercado con una inversión de un millón de dólares estaría dispuesto a prepararse para una pérdida diaria superior a 43,000 dólares con una probabilidad de ocurrencia de 1,42 % conforme indica el ES, un 13 % de capital extra en comparación con los 38,000 dólares que propone el MS en donde se espera que el 97.16 % de las veces no se exceda dicho límite. De esta manera el inversor o entidad financiera obtiene la posibilidad de ajustar mejor sus decisiones de acuerdo a la probabilidad de ocurrencia de los eventos extremos y su perfil de riesgo, lo que invita a pensar en la mediana como una referencia más interesante para el cálculo del valor en riesgo condicional.

2.4 Selección del mejor método

Para evaluar la volatilidad, objetivo final del proceso, fue necesario establecer una estrategia que permitiera identificar el método cuyo valor en riesgo sea la mejor aproximación para pronosticar futuros retornos. Distintos métodos han sido propuestos en la literatura para evaluar la bondad del modelo VaR. Ver por ejemplo, Christoffersen, o el de Kupiec, este último evalúa la proporción de las violaciones al VaR comparando dicha proporción con el nivel de significancia esperado (Leung et al., 2021).

Para la elección del método de mejor ajuste, se realizó un Backtesting usando las 99 observaciones correspondientes a los periodos seis y siete de cada indicador. Se procedió a calcular el VaR con los 19 datos iniciales de modo que, este valor es el VaR esperado para los siguientes 19 días. Usando los 19 datos posteriores, se calculó el VaR real de modo que se hizo la comparación entre el VaR esperado (pronóstico) con las observaciones de los primeros 19 días y el VaR real obtenido con las observaciones de esos días en el archivo de datos. Este procedimiento se realizó cuantas veces fue posible, comenzando períodos nuevos a partir del día dos, tres, etc., en la serie hasta completar los 99 datos. El Valor en Riesgo esperado se calculó con los métodos propuestos (Bootstrap paramétrico y no paramétrico) y la comparación se hizo utilizando el error absoluto medio porcentual (MAPE) como criterio más importante, además de la desviación absoluta media (MAD) y el error cuadrático medio (ECM) como criterios auxiliares. El criterio MAPE consiste en el promedio de los errores porcentuales entre el pronóstico y el valor real, lo cual permite cuantificar la precisión de los métodos comparados en el backtesting. La lógica subyacente es que hallar el valor en riesgo es blindarse de una manera más precisa contra las pérdidas esperadas, de modo que sobreestimar el valor en riesgo sería equivalente a mayor costo de capital y subestimarlo es exponer a pérdidas una mayor parte del capital que lo calculado inicialmente.

3. Resultados

3.1 Resultados del Backtesting

La tabla 3. muestra respectivamente la desviación absoluta media (MAD), el error cuadrático medio (ECM) y el error porcentual absoluto medio (MAPE) donde se puede observar que la distribución normal es la más precisa para los indicadores S&P500 y Dow Jones, y el método no paramétrico usado en este caso es el más preciso para calcular el VaR en los índices COLCAP, VIX y Brent, dicha decisión se toma considerando los métodos con los menores niveles de error, partiendo del MAPE como primer criterio decisorio.

Tabla 3

Tabla 3. Resultados de Backtesting (MAD, ECM y MAPE)

	Índices financieros	No Paramétrico	Normal	Cauchy
Desviación absoluta media MAD	SP	0.010	0.008	2847208744114
	DJ	0.009	0.008	0.069
	COLCAP	0.006	0.006	0.055
	VIX	0.041	0.049	171972826295
	BRENT	0.013	0.014	0.165
Error cuadrático medio ECM	SP	0.000	0.000	494502455586050000000000000
	DJ	0.000	0.000	0.006
	COLCAP	0.000	0.000	0.004
	VIX	0.002	0.003	1804053832009030000000000
	BRENT	0.000	0.000	0.040
Error porcentual absoluto medio MAPE	SP	0.854	0.749	341146238763669
	DJ	0.678	0.656	5.510
	COLCAP	0.684	0.686	5.309
	VIX	0.575	0.740	3499417553388
	BRENT	0.717	0.825	7.766

Tabla 4

Tabla 4. Verificación de VaR y CVaR en su intervalo

	¿Está en el intervalo de VaR generado desde datos 2019?		¿Está en el intervalo de CVaR generado desde datos 2019?
Periodos	Distribución normal (SP, DJ) Distribución no paramétrica (COLCAP, VIX., BRENT)	Datos reales 2020	Distribución normal (SP, DJ) Distribución no paramétrica (COLCAP, VIX, BRENT)	Datos reales 2020
SP2020	NO	NO	NO	NO
DJ2020	NO	NO	NO	NO
COLCAP2020	NO	NO	NO	NO
VIX2020	SÍ	SÍ	SÍ	SÍ
BRENT2020	NO	NO	NO	NO
SP4	NO	NO	NO	NO
DJ4	NO	NO	NO	NO
COLCAP4	NO	NO	NO	NO
VIX4	NO	NO	NO	NO
BRENT4	NO	NO	NO	NO
SP5	NO	NO	NO	NO
DJ5	NO	NO	NO	NO
COLCAP5	NO	NO	NO	NO
VIX5	NO	NO	NO	NO
BRENT5	NO	NO	NO	NO
SP6	SÍ	SÍ	SÍ	NO
DJ6	NO	SÍ	NO	NO
COLCAP6	SÍ	NO	NO	NO
VIX6	NO	NO	SÍ	SÍ
BRENT6	SÍ	SÍ	SÍ	SÍ

Nota. La Tabla 4. muestra la existencia o no existencia de un VaR y MS calculado para los índices financieros en los periodos y subperiodos del año 2020 dentro del intervalo de confianza VaR y MS originado a partir de los periodos y subperiodos del año 2019. Fuente: Elaboración propia

Tabla 5

Tabla 5.Impacto en el intervalo

Periodos	Rango del intervalo VaR	variación	Rango del intervalo CVaR	variación
SP2019	0.0057		0.0069
SP2020	0.0187	227.89 %	0.0242	251.98 %
SP1	0.0085		0.0093
SP4	0.0302	256.99 %	0.0330	253.58 %
SP2	0.0083		0.0102
SP5	0.0690	729.30 %	0.0808	694.99 %
SP3	0.0080		0.0100
SP6	0.0110	36.48 %	0.0134	33.02 %
DJ2019	0.0055		0.0068
DJ2020	0.0201	263.34 %	0.0262	284.94 %
DJ1	0.0104		0.0114
DJ4	0.0329	216.61 %	0.0356	212.75 %
DJ2	0.0080		0.0096
DJ5	0.0728	804.47 %	0.0879	818.80 %
DJ3	0.0077		0.0097
DJ6	0.0124	60.52 %	0.0156	60.20 %
COLCAP2019	0.0110		0.0125
COLCAP2020	0.0720	554.09 %	0.0800	540.00 %
COLCAP1	0.0090		0.0085
COLCAP4	0.0144	60.00 %	0.0115	35.29 %
COLCAP2	0.0155		0.0125
COLCAP5	0.0840	441.94 %	0.0560	348.00 %
COLCAP3	0.0135		0.0150
COLCAP6	0.0190	40.74 %	0.0330	120.00 %
VIX2019	0.0570		0.0785
VIX2020	0.0550	–3.60 %	0.0680	–13.38 %
VIX1	0.0250		0.0190
VIX4	0.1262	404.80 %	0.1030	442.11 %
VIX2	0.0630		0.0485
VIX5	0.1800	185.71 %	0.1660	242.27 %
VIX3	0.0910		0.0920
VIX6	0.0434	–52.31 %	0.0560	–39.13 %
BRENT2019	0.0170		0.0155
BRENT2020	0.0643	277.94 %	0.2010	1196.77 %
BRENT1	0.0310		0.0265
BRENT4	0.0420	35.48 %	0.0390	47.17 %
BRENT2	0.0080		0.0055
BRENT5	0.1874	2241.88 %	0.1710	3009.09 %
BRENT3	0.0178		0.0400
BRENT6	0.0452	154.65%	0.0520	30.00%

Nota. La Tabla 5. muestra los rangos del VaR y MS aplicados a los índices financieros. Cada intervalo surge a partir de los percentiles 0.025 y 0.975 de los grupos VaR y MS. Las variaciones porcentuales comparan los periodos y subperiodos del año 2020 con sus análogos en el año anterior 2019. Lo anterior se calcula como, donde R representa el rango calculado para un periodo t. Fuente: Elaboración propia

El rango de los intervalos es fiel reflejo de la variabilidad en cada periodo e indicador estudiado, es por ese motivo que se procede a analizar la variación presentada en cada rango con el propósito de evaluar el impacto de los eventos anexos a dicho espacio temporal.

De acuerdo con los resultados presentados en la Tabla 4. no se logra anticipar el VaR o CVaR de referencia para los retornos ocurridos en los subperiodos cuatro y cinco del año 2020 en los índices S&P500, Dow Jones, COLCAP y precios del petróleo Brent, se puede evidenciar que con los métodos usados y aunque se genere intervalos de un nivel de confianza del 95 %, resultan ineficaces para predecir la magnitud de los efectos ocasionados por la pandemia, finalmente, cualquier pronóstico ha de ser poco útil cuando un evento de estas características se presenta. Es importante resaltar que los valores de referencia VaR y MS generados en el periodo seis para algún indicador en por lo menos un caso propuesto, se ubica dentro de lo esperado según las proyecciones originadas en el periodo tres, esto puede ser tomado como indicio de un retorno a la estabilidad. Como ejemplo de lo anterior se puede señalar que el VaR generado para el índice COLCAP a partir de un periodo seis y por medio del uso del método no paramétrico (-0.024) se encuentra en el intervalo [-0.027 - (-0.012)], intervalo originado desde el uso del método no paramétrico para los retornos propios del periodo tres.

Los resultados obtenidos demuestran un aumento en los rangos predeterminados desde el periodo 2019 en comparación con los rangos que pueden calcularse a partir del historial de los datos del año 2020, es así como se puede observar que para un nivel de confianza del 95 % el rango más afectado es el del precio del petróleo de referencia Brent con un aumento equivalente a más de 22 veces el rango proyectado para su VaR desde el periodo dos y un aumento de más de 30 veces su rango para el caso del MS. Los resultados de las variaciones de los rangos muestran un notable impacto de los hechos ocurridos en el periodo comprendido entre el 6 de marzo hasta el 21 de abril del 2020 (periodo cinco), periodo de conflictos encabezados por Arabia Saudita y Rusia, países que impedían un acuerdo de recorte en la producción de crudo, referente a lo anterior históricamente se habla de la existencia de una correlación negativa entre los precios del crudo y diversos mercados financieros que principalmente son consumidores, se dice que un aumento en los precios del petróleo encarece la producción industrial generando una reducción de márgenes y con ello la baja en las proyecciones de rentabilidad, sin embargo, para los mercados de Colombia y Norteamérica en los periodos analizados se puede inferir todo lo contrario, es así como el fenómeno observado en el periodo cinco, muestra movimientos a la baja, y consecuentemente aumentos en el valor en riesgo tanto para el precio del petróleo como para los índices Dow Jones, S&P500 y COLCAP. Como hipótesis se tiene que las disminuciones en la demanda industrial a causa del COVID-19 ocasionaron cierta interacción temporal más clara entre el precio del petróleo y los mercados, se presume entonces que las medidas gubernamentales y globales dadas para afrontar la pandemia aportaron al hundimiento de los precios del petróleo, al tiempo que las especulaciones financieras traían una tendencia bajista en los rendimientos.

Ahora bien, las cifras de muertes reportadas por el gobierno de Estados Unidos dentro del periodo evaluado muestran su pico más alto el 21 de abril del año 2020, a partir de dicha fecha se observaron reducciones frecuentes en las cifras diarias de los tres meses siguientes y con ello un mayor optimismo por parte de los inversores, dichos eventos estuvieron acompañados del anuncio de medidas monetarias expansivas por parte de la reserva federal de Estados Unidos(FED), ayudando al crecimiento y estabilización de los índices referentes a la potencia mundial.

Tabla 6

Tabla 6. Comparación entre periodos análogos

Periodos de comparación	VaR con distribución normal en ambos periodos	VaR con distribución normal en los periodos 2019 y VaR con datos reales en los periodos 2020	VaR con datos reales del 2019 y 2020	MS con distribución normal en ambos periodos	MS con distribución normal en los periodos 2019 y MS con datos reales en los periodos 2020	MS con datos reales del 2019 y 2020
SP2019 vs SP2020	242.69 %	250.32 %	275.00 %	247.18 %	281.96 %	183.72 %
SP1 vs SP4	449.70 %	456.90 %	770.00 %	416.92 %	413.21 %	515.38 %
SP2 vs SP5	861.87 %	965.19 %	1107.33 %	822.35 %	963.46 %	744.44 %
SP3 vs SP6	16.11 %	11.10 %	5.00 %	19.47 %	34.50 %	–3.85 %
DJ2019 vs DJ2020	268.86 %	247.58 %	222.14 %	275.65 %	341.89 %	238.10 %
DJ1 vs DJ4	337.51 %	328.81 %	386.49 %	318.51 %	292.73 %	376.47 %
DJ2 vs DJ5	926.01 %	996.00 %	1156.00 %	899.61 %	1042.21 %	834.62 %
DJ3 vs DJ6	42.00%	23.83%	6.67%	44.79%	53.26%	16.67%

Nota. La Tabla 6. muestra la variación porcentual del VaR y MS calculado para los índices financieros en los periodos y subperiodos del año 2019 contrastando con el VaR y MS calculado en los periodos y subperiodos del año 2020. Fuente: Elaboración propia

Tabla 7

Tabla 7. Comparación entre periodos análogos

Periodos de comparación	VaR con distribución no paramétrico en ambos periodos	VaR con distribución no paramétrico en los periodos 2019 y VaR con datos reales en los periodos 2020	VaR con datos reales del 2019 y 2020	MS con distribución no paramétrico en ambos periodos	MS con distribución no paramétrico en los periodos 2019 y MS con datos reales en los periodos 2020	MS con datos reales del 2019 y 2020
COLCAP1 vs COLCAP4	215.09 %	247.66 %	260.36 %	169.69 %	194.16 %	158.82 %
COLCAP2 vs COLCAP5	508.42 %	547.50 %	446.83 %	491.26 %	517.00 %	472.09 %
COLCAP3 vs COLCAP6	60.47 %	74.13 %	89.09 %	52.01 %	58.34 %	39.13 %
VIX2019 vs VIX2020	3.77 %	3.48 %	3.76 %	1.21 %	–1.15 %	1.08 %
VIX1 vs VIX4	65.19 %	71.25 %	62.35 %	82.44 %	97.67 %	91.12 %
VIX2 vs VIX5	69.45 %	56.91 %	48.56 %	89.18 %	101.40 %	85.00 %
VIX3 vs VIX6	–32.22 %	–34.68 %	–35.70 %	–33.93 %	–28.03 %	–33.14 %
BRENT2019 vs BRENT2020	150.07 %	141.94 %	134.12 %	251.44 %	207.60 %	213.16 %
BRENT1 vs BRENT4	111.33 %	91.75 %	120.36 %	98.65 %	112.18 %	96.23 %
BRENT2 vs BRENT5	1893.70 %	2078.86 %	1962.86 %	1991.39 %	2324.34 %	2124.00 %
BRENT3 vs BRENT6	11.54%	11.45%	8,80%	25.69%	28.25%	33.33%

Nota. La Tabla 7. muestra la variación porcentual del VaR y MS calculado para los índices financieros en los periodos y subperiodos del año 2019 contrastando con el VaR y MS calculado en los periodos y subperiodos del año 2020. Fuente: Elaboración propia

En las Tablas 6 y 7 es posible observar un comportamiento creciente en el valor en riesgo calculado para todos los indicadores en los periodos cuatro y cinco del año 2020 comparados con los periodos uno y dos sus análogos en el año 2019 al igual que decrecimiento para el VIX en el periodo seis. Al observar el impacto de la volatilidad en el periodo cinco y tomando como punto de comparación el periodo dos (periodo análogo), se tiene que el índice S&P500 y el Dow Jones tienen un aumento de 11 veces su VaR. El VaR para el índice COLCAP casi llega a aumentar cinco veces su valor absoluto y finalmente el VaR calculado para los precios de petróleo Brent llegan casi a multiplicarse 20 veces mientras su CVaR lo hace 21 veces. Siendo el precio del petróleo Brent el de mayor afectación, se evidenció que la proporción de ocasiones en que sus retornos superan los límites del VaR en el periodo cinco es del 57 %, mientras se esperaba que solamente ocurriera en máximo un 5 % de las ocasiones según datos del periodo dos.

El periodo seis es el periodo con las menores variaciones respecto a lo previsto desde los datos de su periodo análogo en el año 2019. Diversos hechos pueden justificar el alivio del mercado norteamericano en dicho periodo, por ejemplo, un mayor consumo del crudo en la economía contribuyó al sentimiento de recuperación reflejado en el mercado. Por otro lado, el mercado colombiano recibía el efecto de las restricciones y la cuarentena, y a pesar de las recuperaciones en el precio del petróleo, materia prima que representa directamente la principal contribución de las finanzas estatales, no se percibían grandes reversiones hacia una tendencia positiva en los retornos del índice COLCAP.

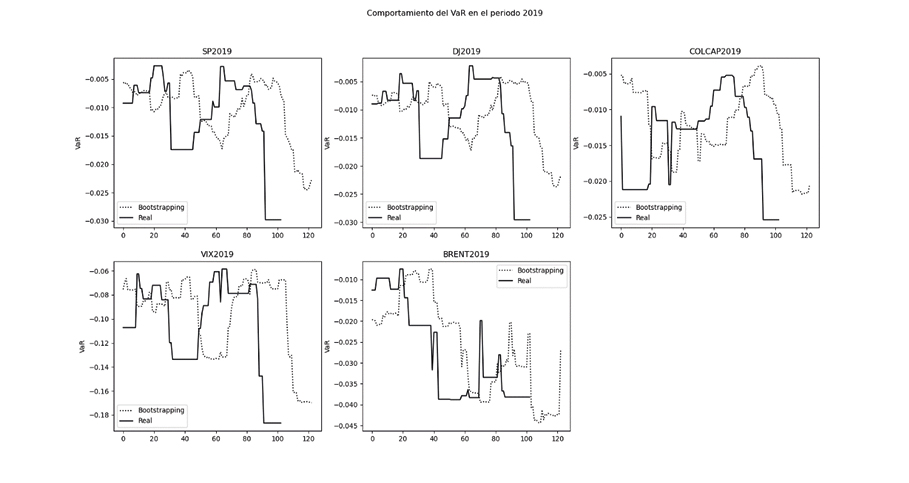
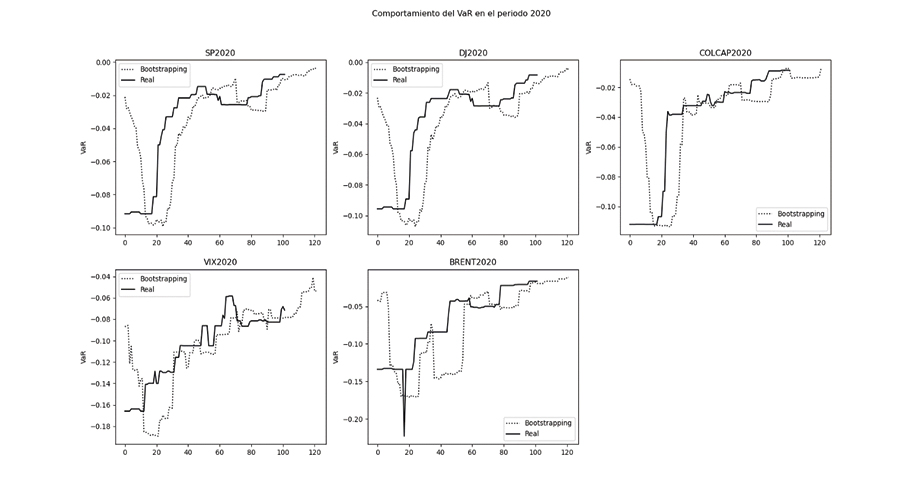
Graficando el VaR para cada indicador en el periodo 2019 y 2020, y con una muestra variable de 19 días, se puede observar que para el periodo 2019 el VaR de los índices S&P500, Dow Jones, COLCAP y precio del petróleo Brent suelen mantenerse sin variaciones abruptas, logrando estar siempre por encima de -0.04, sin embargo, para el periodo 2020 y tomando como referencia el precio del petróleo, se tiene que su VaR desciende a hasta por debajo de -0.14, lo que significa más de tres veces su valor en periodos habituales (asumiendo como tal el año 2019) es así como la forma convexa que se obtiene al inicio de la gráfica y que se replica para el resto de índices tratados, muestra no solo un fuerte impacto negativo en los retornos y por ende en el cálculo del VaR, sino que también es una muestra de una fuerte recuperación de los mismos.

Gráfica 2

Gráfica 2. Comportamiento del VaR en el periodo 2019

Fuente: Elaboración propia

Gráfica 3

Gráfica 3. Comportamiento del VaR en el periodo 2020

Fuente: Elaboración propia

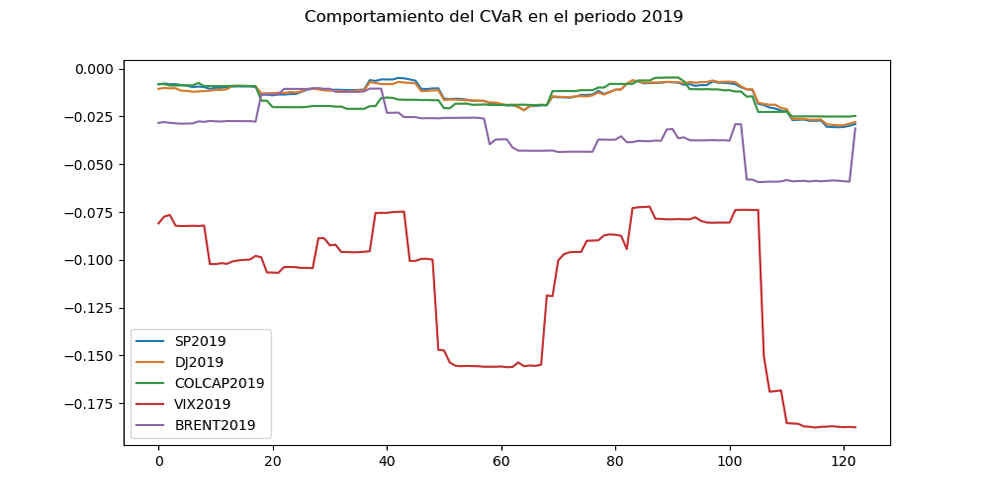
Revisando la gráfica 4 y 5 perteneciente al MS para el periodo 2019 y 2020 respectivamente, se evidencia un comportamiento completamente análogo al del VaR, sin embargo, se hace notoria la aparición de rendimientos de menor cuantía como era de esperarse.

Gráfica 4

Gráfica 4. Comportamiento del MS en el periodo 2019

Fuente: Elaboración propia

Gráfica 5

Gráfica 5. Comportamiento del MS en el periodo 2020

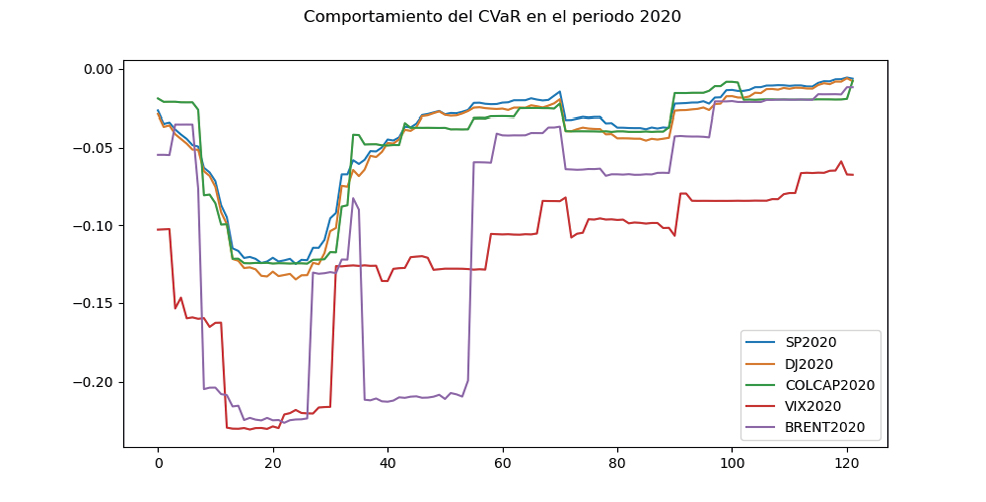
Fuente: Elaboración propia

4. Discusión y conclusiones

La confiabilidad en el uso del valor en riesgo para periodos de crisis resulta ser reducida en contraste con periodos de estabilidad económica, tal como se vio reflejado en la confrontación entre los indicadores de riesgo y sus intervalos de confianza en los periodos evaluados. La evidencia en el periodo 2020 demuestra movimientos poco predecibles para cada uno de sus subperiodos y el análisis comparativo realizado respecto al periodo 2019 deja claro la magnitud de los impactos por los eventos considerados. La variación del VaR y MS es ocasionada por la volatilidad de los mercados en los periodos observados, dicha volatilidad es a su vez sinónimo de movimientos erráticos y difíciles de predecir en los rendimientos diarios de los índices, dando paso a grandes cuestionamientos para los inversores, quienes deben decidir cuánto riesgo están dispuestos a asumir y preguntarse si eventos parecidos a los revisados en este artículo tendrían comportamientos análogos en un futuro, de ser así las medidas de riesgo documentadas en esta crisis funcionarían como precedente.

A partir de los resultados del análisis empírico, es posible decir que las medidas de riesgo estándar como VaR y MS pueden ser útiles en escenarios de relativa calma, pero no son suficientes para proyectar medidas ante escenarios de turbulencia, escenarios que, de sostenerse durante tiempos prolongados, harían necesario el fortalecimiento patrimonial de entidades financieras cuyas carteras dependen de estos índices analizados o de las especies que los componen. También es importante considerar el rezago temporal que propician estas medidas, que irónicamente advierten del riesgo cuando el evento ya ha ocurrido. En tal caso, la búsqueda de metodologías que logren captar el riesgo frente a las posibles variaciones en el incremento de la volatilidad, son pertinentes para la gestión del riesgo en tiempos donde la globalización ha traído posiblemente como resultado colateral, la capacidad de generar un efecto contagio en los mercados financieros, es decir un acrecentamiento de sus correlaciones en periodos de extrema volatilidad.

El periodo 2020 se caracterizó no solo por tener grandes caídas en los índices de referencia, si no por grandes recuperaciones como las observadas en el mercado norteamericano, una vez más lo que inicialmente fue un escenario pesimista termina transformándose en uno optimista, donde la reversión de la tendencia negativa del VaR conserva el suficiente impulso como para estabilizar de nuevo los valores regulares registrados en el año 2019. Entre el conjunto de estrategias utilizadas para dinamizar la economía norteamericana se encuentran la disminución de las tasas de interés por parte de la FED; el tipo de interés a inicios del año 2019 se ubicaba en 2.25 %, luego el 3 de marzo del año 2020 pasa a ser 1 %, y finalmente el 16 de marzo del 2020 llega a un 0 %, en dicho punto también se anunció una inyección de liquidez por 1.5 billones de dólares, esta última medida intensifica los montos ya usados en la denominada “Flexibilización Cuantitativa”, lo que en conjunto activó la demanda, permitiendo la refinanciación de las entidades bancarias y a su vez la recuperación de los índices norteamericanos, puesto que en parte de los cálculos ya en un nivel corporativo, se contempla que el uso de deuda apalanca la recompra de acciones y en consecuencia, el crecimiento esperado en el valor de las empresas ocasiona la reversión en la tendencia negativa de los índices, de esta forma por ejemplo, el índice S&P500 logra alcanzar su máximo histórico para ese momento, el 26 de agosto del año 2020. El Banco de la República de Colombia por su parte toma medidas en su tipo de interés, reduciendo en 50 puntos básicos desde inicios del año 2020 hasta finales de marzo de 2020, esta medida pudo haber sumado a la recuperación del índice COLCAP en los meses posteriores, no obstante, es el alza de los precios del petróleo el factor más relevante en la recuperación percibida.

Una de las bondades que se le puede sumar al MS sobre el Déficit Esperado (ES) consiste en la preparación de requisitos de capital para un evento de mayor probabilidad de ocurrencia. El hecho de usar la mediana en lugar de la media es pertinente cuando se tratan distribuciones asimétricas con concentraciones en los extremos, tal como es el caso de las colas de las distribuciones pertenecientes a los rendimientos financieros; naturalmente la media tiende a desviarse frente a variaciones extremas, aunque dichas variaciones tuvieran una probabilidad muy pequeña de repetirse, esto provoca una proyección que sobrevalora el riesgo, en contraste, la mediana no posee tal sensibilidad ante los valores extremos, entonces esta medida podrá pronosticarse con mayor certeza y sin sufrir grandes alteraciones que afecten drásticamente la probabilidad calculada de eventos futuros, el anterior enunciado tiene una fuerte repercusión en el manejo del capital invertido y permitiría que el uso mesurado de los flujos de capital para blindarse del riesgo genere mejores resultados en el rendimiento esperado.

La crisis ocasionada por la pandemia del COVID-19 dejó los niveles más bajos en los precios del petróleo en toda la historia y simultáneo a esto ocasionó una tendencia negativa en el resto de los indicadores tratados, a su vez el periodo con niveles VaR de precios del petróleo más pesimistas coincide con el periodo de conflictos entre Rusia y Arabia Saudita, es así como las implicaciones a los mercados bursátiles son una importante muestra de la sensibilidad de los inversores hacia el entorno y representan un indicio claro de la manera en que estos reaccionan respecto a los movimientos del precio del petróleo reforzando el argumento que apunta a una fuerte relación entre los mercados y el crudo aún existente hasta estos tiempos.

El VaR asociado al índice COLCAP perteneciente al mercado de Colombia obtuvo movimientos miméticos al VaR originado de los índices norteamericanos en los periodos estudiados, esto puede ser resultado de una reacción paralela a los cambios del entorno o a un estado coercitivo donde los cambios en la volatilidad de los mercados de Estados Unidos influyen sobre las reacciones del mercado de Colombia. Este comportamiento debe estudiarse más a fondo y extenderse al resto de mercados latinoamericanos, lo anterior es relevante para entender la dependencia existente entre los mercados de la región y el análisis de las correlaciones prevalecientes, ya sea en tiempos de estabilidad económica o en periodos volátiles, esto puede otorgar indicios de la dirección que están tomando los mercados financieros implicados.

5. Recomendaciones y Trabajos Futuros

El análisis de otros índices puede enriquecer los resultados de investigaciones futuras, haciendo uso de las herramientas de medición del riesgo sobre variables que intervienen en la clase de eventos tratados, como por ejemplo el índice del dólar (DXY), índice que compara el valor del dólar estadounidense referente a otras monedas de importancia global, el cual ha tenido un cambio muy importante en tiempos recientes.

Respecto a los modelos de pronóstico que se pueden generar, o que pueden ser candidatos para la proyección del VaR y CVaR se encuentran los modelos de volatilidad GARCH, sus ventajas han sido evaluadas por otros autores y su ajuste a los mercados emergentes o latinoamericanos puede contribuir a la discusión en trabajos futuros.

REFERENCIAS

Ahmed, D., Soleymani, F., Ullah, M. Z., & Hasan, H. (2021). Managing the risk based on entropic value-at-risk under a normal-Rayleigh distribution. Applied Mathematics and Computation, 402, 126129. https://doi.org/10.1016/j.amc.2021.126129

Alonso, J. C., & Chaves, J. M. (2013). Value-at-risk: Evaluation of the behavior of different methodologies for 5 Latin American countries. Estudios Gerenciales, 29(126), 37–48. https://doi.org/10.1016/S0123-5923(13)70018-4

Ardia, D., & Hoogerheide, L. F. (2014). GARCH models for daily stock returns: Impact of estimation frequency on Value-at-Risk and Expected Shortfall forecasts. Economics Letters, 123(2), 187–190. https://doi.org/10.1016/j.econlet.2014.02.008

Bourghelle, D., Jawadi, F., & Rozin, P. (2021). Oil price volatility in the context of Covid-19. International Economics, 167(April), 39–49. https://doi.org/10.1016/j.inteco.2021.05.001

Chernick, M. R. (2008). Bootstrap Methods: A Guide for Practitioners and Researchers by CHERNICK, M. R. Biometrics, 64(3), 998–999. https://doi.org/10.1111/j.1541-0420.2008.01082_17.x

Davison, A. C., & Hinkley, D. V. (1997). The Basic Bootstraps. In Bootstrap Methods and their Application (pp. 11–69). Cambridge University Press. https://doi.org/10.1017/CBO9780511802843.003

Efron, B. (2007). Bootstrap Methods: Another Look at the Jackknife. The Annals of Statistics, 7(1), 1–26. https://doi.org/10.1214/aos/1176344552

Tibshirani, R. J., & Efron, B. (1993). An introduction to the bootstrap. Monographs on statistics and applied probability, 57(1). 1-436

Erdely, A. (2017). Valor en riesgo y el dogma de la diversificación. Revista De Métodos Cuantitativos Para La Economía Y La Empresa, 24, Páginas 209 a 219. https://doi.org/10.46661/revmetodoscuanteconempresa.2888

Feria Domínguez, J. M. (2005). El Riesgo de mercado: su medición y control. In Delta Publicaciones (Ed.), Finanzas para la nueva economía. (N.o 1 edic).

Geenens, G., & Dunn, R. (2022). A nonparametric copula approach to conditional Value-at-Risk. Econometrics and Statistics, 21, pp. 19 – 37. https://doi.org/10.1016/j.ecosta.2020.07.001

Google Finance. (2021). https://www.google.com/finance/

Investing. (2021). https://es.investing.com/

Josaphat, B. P., & Syuhada, K. (2021). Dependent conditional value-at-risk for aggregate risk models. Heliyon, 7(7). e07492. https://doi.org/10.1016/j.heliyon.2021.e07492

Kim, D., & Kang, K. H. (2021). Conditional value-at-risk forecasts of an optimal foreign currency portfolio. International Journal of Forecasting, 37(2), 838–861. https://doi.org/10.1016/j.ijforecast.2020.09.011

Kou, S., & Heyde, C. C. (2013). External Risk Measures and Basel Accords Mathematics of Operations Research, 38 (3). https://www.jstor.org/s. 38(3), 393–417.

Leung, M., Li, Y., Pantelous, A. A., & Vigne, S. A. (2021). Bayesian Value-at-Risk backtesting: The case of annuity pricing. European Journal of Operational Research, 293(2), 786–801. https://doi.org/10.1016/j.ejor.2020.12.051

Li, L. (2017). Testing and comparing the performance of dynamic variance and correlation models in value-at-risk estimation. North American Journal of Economics and Finance, 40, 116–135. https://doi.org/10.1016/j.najef.2017.02.006

Lorenzo Valdés, Arturo. (2016). Exceso de confianza como determinante de la volatilidad en mercados accionarios latinoamericanos. Contaduría y administración, 61(2), 324-333. https://doi.org/10.1016/j.cya.2015.11.006

Meng, X., & Taylor, J. W. (2018). An approximate long-memory range-based approach for value at risk estimation. International Journal of Forecasting, 34(3), 377–388. https://doi.org/10.1016/j.ijforecast.2017.11.007

Oxford Business Group. The Report: Colombia 2013: Country Profile. https://oxfordbusinessgroup.com/colombia-2013

Ozkan, O. (2021). Impact of COVID-19 on stock market efficiency: Evidence from developed countries. Research in International Business and Finance, 58(April), 101445. https://doi.org/10.1016/j.ribaf.2021.101445

Rodríguez, G. (2017). Teoría de valores extremos: una aplicación a los retornos bursátiles peruanos. Revista De Métodos Cuantitativos Para La Economía Y La Empresa, 23, Páginas 48 a 74. https://doi.org/10.46661/revmetodoscuanteconempresa.2686

Sarwar, S., Shahbaz, M., Anwar, A., & Tiwari, A. K. (2019). The importance of oil assets for portfolio optimization: The analysis of firm level stocks. Energy Economics, 78, 217–234. https://doi.org/10.1016/j.eneco.2018.11.021

So, M. K. P., & Yu, P. L. H. (2006). Empirical analysis of GARCH models in value at risk estimation. Journal of International Financial Markets, Institutions and Money, 16(2), 180–197. https://doi.org/10.1016/j.intfin.2005.02.001

Johnson, N. L., Kotz, S., & Balakrishnan, N. (1995). Continuous univariate distributions, volume 2 (2nd ed). John Wiley & Sons.

Wei, Y., Qin, S., Li, X., Zhu, S., & Wei, G. (2019). Oil price fluctuation, stock market and macroeconomic fundamentals: Evidence from China before and after the financial crisis. Finance Research Letters, 30(January), 23–29. https://doi.org/10.1016/j.frl.2019.03.028

World Health Organization. (3 de marzo de 2020). Coronavirus disease 2019 (COVID-19) Situation Report-43.

Xu, Y., Wang, X., & Liu, H. (2021). Quantile-based GARCH-MIDAS: Estimating value-at-risk using mixed-frequency information. Finance Research Letters, 1, 101965. https://doi.org/10.1016/j.frl.2021.101965

Zhang, J. (2010). A highly efficient L-estimator for the location parameter of the Cauchy distribution. Computational Statistics, 25(1), 97–105. https://doi.org/10.1007/s00180-009-0163-y