Modelos de Programación Entera para el Problema de Asignación de Horarios en Cursos Universitarios
Integer Programming Model for the Timetabling Problem in University Courses
Carlos Andrés Arango Londoño
Universidad de La Salle (Colombia)
https://orcid.org/0000-0002-6026-3107
Heriberto Felizzola Jiménez
Universidad de La Salle (Colombia)
https://orcid.org/0000-0003-3149-8182
Andrés Hualpa Zuñiga
Universidad de La Salle (Colombia)
https://orcid.org/0000-0002-5232-6526
Paula Z. Gómez Martínez
Carvajal Tecnología y Servicios (Colombia)
https://orcid.org/0000-0003-0835-0956
Carlos Mora Garzón
Colsubsidio (Colombia)
https://orcid.org/0000-0002-3533-6845
RESUMEN
La programación de horarios se clasifica como un problema combinatorio para el que existen múltiples alternativas de solución incluyendo entre ellas la programación entera. Sin embargo, el modelado de reglas operativas y el tamaño de problemas reales hace que su uso no sea común comparado con otras técnicas. El presente artículo propone un modelo de programación entera (IP), que aborda el problema de programación de horarios conformado por variables asociadas con franjas horarias, asignatura y docente asignado. También se incluyen parámetros como número de franjas horarias mínimas y máximas a impartir por el docente, tiempo de franja horaria, disponibilidad de docente, salones disponibles y costo estimado de insatisfacción generado por el horario asignado. En el modelo se integran siete restricciones duras y diecisiete blandas que proporcionan mayor calidad a la solución final de horarios. Se valida el modelo IP con una función objetivo global, en el que se reportan experimentos y resultados obtenidos en instancias reales de la Universidad de la Salle (ULS). El nuevo enfoque de solución ofrece mejoras en los horarios finales, así como la interacción con los usuarios durante su construcción. Finalmente, en las conclusiones del trabajo se discute el diseño y desarrollo de un sistema que brinda soporte a las decisiones, referenciando sugerencias para futuros desarrollos.
PALABRAS CLAVE
Programación de horarios; programación entera; asignación de cursos.
ABSTRACT
Timetabling scheduling is classified as a combinatorial problem for which there are multiple solution alternatives, including the integer programming. However, the modeling of operational rules and the size of real problems makes its use not common compared to other techniques. This article proposes an integer programming model (IP) model, which addresses the scheduling problem made up of variables associated with time slots, subject and assigned teacher. Parameters such as the number of minimum and maximum time slots to be taught by the teacher, time slot time, teacher availability, available classrooms and estimated cost of dissatisfaction generated by the assigned schedule are also included. Seven hard and seventeen soft constraints are integrated into the model, which provide higher quality to the final schedule solution. The IP model is validated with a global objective function, in which experiments, and results obtained in real instances of the Universidad de la Salle (ULS) are reported. The new solution approach offers improvements in the final schedules, as well as the interaction with the users during its construction. Finally, in the conclusions of the work, the design and development of a system that provides support for decisions is discussed, referencing suggestions for future developments.
KEYWORDS
Timetabling; integer programming; classroom assignment.
Clasificación JEL: C610
MSC2010: 90C11
1. Introducción
Las universidades e instituciones académicas se ven enfrentadas al problema de programar semestre a semestre sus recursos de infraestructura y talento humano para brindar un servicio de educación a sus estudiantes (Usuarios). De este proceso se deriva la actividad de programación de horarios para cursos universitarios (University Course Timetabling Problem, “UCTTP”) en el que se asignan docentes y aulas para impartir clases a lo largo de un periodo académico.
Una práctica frecuente para esta actividad es realizarla de manera manual usando formatos montados en hojas de cálculo. Este método permite al programador cruzar o reasignar los horarios, docentes y aulas cumpliendo con restricciones como el número máximo de horas que se puede asignar al docente por su condición contractual, evitar el cruce de horarios a estudiantes que vienen nivelados en un semestre, tener asignaturas que requieren de franjas o bloques de dos o más horas según la intensidad horaria, ajustar la asignación de acuerdo a la disponibilidad de aulas, definir horas franja para momentos de descanso o alimentación, entre otras. Sin embargo, este método demanda una cantidad considerable de tiempo para establecer una solución aceptable comparado con el tiempo que tomaría al apoyarse con sistemas informáticos más robustos.
En la literatura se identifica que el desarrollo de sistemas informáticos en este ámbito ha tenido fundamento desde las técnicas de investigación de operaciones como un caso complejo de optimización, buscando el objetivo de encontrar una solución que permita asignar eventos que programen franjas horarias y salas predefinidas donde se deben satisfacer todas las restricciones (Tan et al., 2021; Zhu et al., 2021). Los eventos incluyen estudiantes y profesores donde los recursos abarcan las instalaciones y equipos de las aulas, salas teóricas y prácticas. A pesar de que existe un número variado de soluciones de optimización que abordan el problema de programación de horarios, aún se presentan brechas de adaptabilidad de estos es sistemas informáticos, debido al amplio número de restricciones que hay que tener en cuenta para acercarse a la realidad de este proceso.
Este artículo propone un modelo de programación entera para asignar los horarios del Programa de Ingeniería Industrial de la Universidad de La Salle, sede Bogotá. Este modelo sugiere un enfoque de solución alternativo al propuesto por (Torres-Ovalle et al., 2014), demostrando posibilidad de ajuste en las funciones de penalización utilizadas para determinar los valores de los coeficientes de costo, mejorando la calidad de los horarios resultantes. Adicionalmente, cuando el tiempo de cómputo no sea una carga, se pueden agregar nuevos requisitos al cronograma para hacerlos más aceptables por todos los usuarios involucrados.
La sección 2 del artículo describe la problemática presentada en la programación de cursos universitarios. La sección 3, presenta los supuestos, así como las reglas estrictas y blandas del problema de horarios. Se concluye con la definición de las variables binarias a utilizar en la formulación del modelo IP. Finalmente, en la sección 4 se analizan los resultados de la programación resultante revisando el desempeño del modelo en un caso de aplicación.
2. Antecedentes
La programación de tareas es una actividad ampliamente requerida por la industria en general. Este problema ha sido trabajado para el desarrollo de proyectos con restricciones de recursos (Brucker et al., 1999; Neumann et al., 2003); asignación de fuerza laboral (Castillo-Salazar et al., 2016; Hung & Emmons, 1993); agenda de citas en sistemas de salud por su impacto en el desempeño de las instalaciones médicas (LaGanga & Lawrence, 2012; Zacharias & Pinedo, 2014), asignación de horarios en instituciones de educación (Vermuyten et al., 2016) y programación de transporte (de Palma & Lindsey, 2001; Wirasinghe, 2002), específicamente control de trenes (Scheepmaker et al., 2017; Wang & Goverde, 2019), control aéreo (Barnhart et al., 1998) y control marítimo.
En el campo académico, la programación de tareas también ha sido objeto de interés por la comunidad científica, siendo abordado inicialmente como el problema UCTTP (Gotlieb, 1962), bajo la asignación de recursos con capacidad limitada (Profesores, Salones, laboratorios) a tareas o eventos. A partir de la década de los años 60 se usa los gráficos de redes basados en investigación de operaciones para realizar la programación de horarios, inicialmente cuando existen cursos asignados previamente (Welsh, 1967) y posteriormente usando grafos no direccionados (de Werra, 1985). En la teoría de grafos los eventos y los espacios de tiempo son considerados como nodos, arcos y colores. Los cursos se asignan a períodos (días y hora) secuencialmente en función de la heurística de coloración de gráficos, por ejemplo: mayor grado, grado de saturación, mayor grado ponderado y grado de color. (Selim, 1988) propuso un enfoque de coloración gráfica (GC) para encontrar soluciones factibles para UCTTP soportado en un algoritmo de dos etapas. En la primera se utiliza el grado de saturación mínima (LSDF) para encontrar soluciones factibles. En la segunda se mejora la calidad de la solución utilizando operadores basados en una permutación de columna (Nandhini, 2019).
El enfoque de Programación Lineal Entera Mixta (MILP) también ha sido aplicado a este problema, ya que se adapta a la búsqueda de soluciones para la asignación de recursos de capacidad limitada (salas, períodos de enseñanza) de modo que se maximice el interés y se minimice el costo. La definición y la solución del problema de programación lineal va a depender de las restricciones impuestas dentro de cada departamento y los objetivos de este, adaptando su formulación a modelos de gran tamaño (Dimopoulou & Miliotis, 2001). Por otra parte, el enfoque metaheurístico basado en soluciones únicas busca el desarrollo de estrategias que permitan desarrollar algoritmos de optimización los cuales a menudo se enfocan en soluciones locales (Sörensen & Glover, 2013). Entre los algoritmos de búsqueda local utilizados se identifica la búsqueda tabú (TS) en el cual el chequeo de las soluciones se hace teniendo en cuenta una lista que permite que el modelo no se queda atascado en soluciones locales (Battiti & Tecchiolli, 1994; Nagata, 2018).
Otras técnicas utilizadas para la solución a este problema son los algoritmos genéticos, colonia de hormigas (ACO), optimización de enjambres de partículas (PSO), recocido simulado (SA) técnicas multicriterio y multiobjetivo, enfoques híbridos o sistemas multiagente distribuidos (Asmuni, 2008; Babaei et al., 2015; Feizi-Derakhshi et al., 2012). El algoritmo genético utiliza el concepto de evolución biológica integrando tres operadores: selección, cruce y mutación para la creación de la población y la selección de las mejores soluciones. Este proceso se repite por un numero de generaciones determinadas (Alnowaini & Aljomai, 2021; Assi et al., 2018). Del mismo modo, la optimización utilizando colonia de hormigas usa los principios de comportamiento de las hormigas las cuales crean sus propias soluciones e intercambian información de la calidad de sus soluciones con otras hormigas artificiales (Goh et al., 2019; Nothegger et al., 2012). Por su parte, la optimización de enjambres de partículas (PSO) utiliza tanto el mejor global actual como el mejor individual en la iteración t. Una de las razones de utilizar mejor al individuo es probablemente aumentar la diversidad en las soluciones de calidad; sin embargo, esta diversidad se simula utilizando cierta aleatoriedad. Este algoritmo presta atención a la exploración y explotación del espacio de búsqueda (Ghalia, 2008; K. Alsmadi et al., 2022). Por otro lado, el recocido simulado (SA) se caracteriza porque en cada paso considera algunos estados vecinos s* del estado actual s, y probabilísticamente decide entre mover el sistema al estado s* o permanecer en el estado s. Su rendimiento depende de las temperaturas inicial y final, el programa de enfriamiento y la definición de las estructuras del vecindario (Ceschia et al., 2012; Goh et al., 2019; Lewis, 2012). Igualmente, los enfoques que utilizan múltiples criterios o múltiples objetivos no tienen una solución única que optimice cada objetivo. Una solución óptima se obtiene si no se pueden mejorar las funciones objetivo sin degradar las otras funciones (Gülcü & Akkan, 2020; Shakibaei et al., 2021).
Finalmente, los enfoques híbridos integran un grupo de alternativas que combinan diferentes categorías de restricciones que se pueden clasificar en duras y blandas, entre ellas, la consecutividad y limitaciones de las sesiones múltiples (Feng et al., 2017), asignación de número de franjas horarias y días laborales en dos fases (Ribić & Konjicija, 2010), equilibrio en asignación de carga y preferencia docente y administrativa según categoría de cursos como criterios de optimización (Domenech & Lusa, 2016; Ismayilova et al., 2007), el número y tamaño de los salones que no excedan la capacidad así como la consecutividad de sesiones de evaluación para estudiantes, configurando así restricciones blandas que apunten a soluciones satisfactorias para diferentes usuarios (McCollum et al., 2012; Saldaña Crovo et al., 2007). Otro resultado de enfoques híbridos es la integración de modelos independientes de programación entera mixta para asignar docentes en sesiones de clase en función de intervalos de tiempo obtenidos en una primera etapa. El enfoque híbrido se presenta ya que se demuestra que la formulación de programación entera mixta original resulta insostenible (Al-Yakoob & Sherali, 2015).
La revisión de términos que describen alcances, técnicas y/o metodologías de solución, se clasifican mediante análisis de coocurrencia en las fuentes referenciadas como se muestra en la Figura 1.
Figura 1. Alcances, técnicas y/o metodologías de solución al problema de programación de horarios
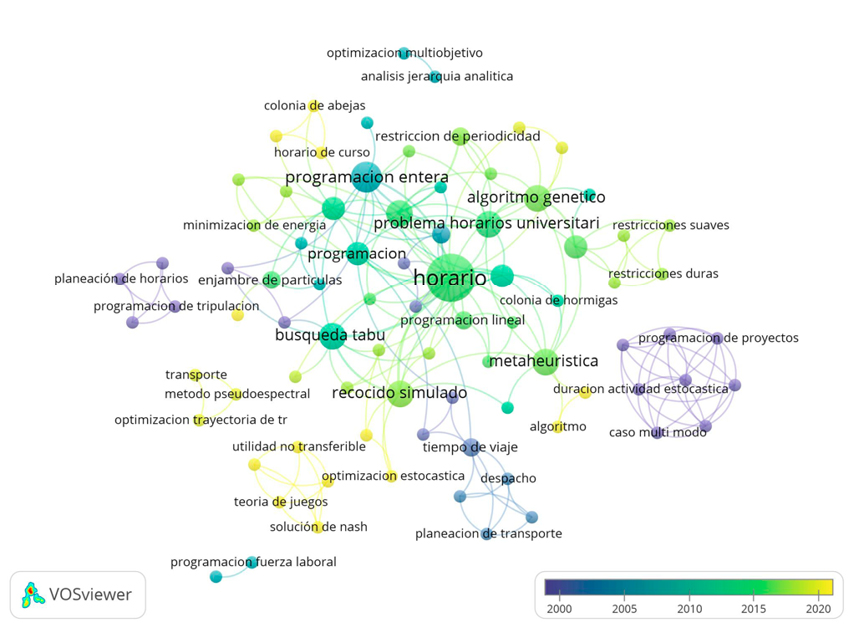
Fuente: Elaboración propia mediante VOSviewer
En la Figura 1 identifica la agrupación de nodos que integran los conceptos más concurridos en la revisión de las fuentes referenciadas, reflejando centralidad en el término “Horario” (Timetabling), del cual se deriva en mayor coocurrencia técnicas de solución como búsqueda tabú, programación entera y mixta, recocido simulado, algoritmo genético y metaheurísticas. En los años más recientes, se mantienen estas técnicas, así como la aplicación de optimización estocástica, teoría de juegos, método pseudo espectral y colonia de abejas.
3. Descripción del Problema
La programación de clases en la Universidad de la Salle es un desafío influenciado por las características de los cursos ofrecidos y los recursos disponibles en la institución. Las clases que ofrece la Universidad pueden incluir clases magistrales ó laboratorios que requieren ser programados en bloques de dos o tres horas consecutivas. Las clases son dirigidas por docentes que trabajan de tiempo completo u ocasionalmente, y estas se programan en una o varias sesiones por semana.
La Universidad cuenta con un sistema de créditos asociados a cada asignatura que influyen en su intensidad horaria. En el caso de Ingeniería Industrial, el número de créditos necesarios para que un estudiante complete sus estudios es de 172 horas. La Universidad clasifica el semestre en el cual se encuentra un estudiante nivelado que, de acuerdo a los créditos aprobados, se presentan restricciones de inscripción para los estudiantes que tienen asignaturas de diferentes semestres. Esto genera la necesidad de establecer una política de programación de horarios que priorice la asignación de asignaturas de modo que no existan cruces entre las que se encuentran en el mismo semestre académico.
Por otra parte, el problema de programación de horarios universitarios requiere de recursos tanto humanos como de infraestructura. En el caso particular, la disponibilidad de recursos en la Universidad de La Salle es determinada por la asignación de tareas administrativas, de investigación y extensión que asume el personal docente. Estas tareas ocupan una serie de períodos durante la semana para cada docente los cuales son establecidos con antelación y que proporcionan parámetros de asignación en períodos de tiempo que limitan la disponibilidad para impartir las clases. Esta limitante de disponibilidad también aplica en infraestructura, específicamente de aulas debido a la franja horaria determinada por la universidad. En la Universidad varios departamentos comparten las aulas, de modo que un departamento tiene acceso a un aula determinada algunos días de la semana y otros departamentos el resto de los días. Reducir el número de estudiantes que quedan sin asignar después de la etapa final requiere ajustes significativos en la cantidad de cursos, profesores y capacidad para ser ocupados en una franja horaria, aumentando la dificultad de la programación. Adicionalmente, la heurística utilizada actualmente carece de la capacidad de manejar varios planes académicos al tiempo, hoy en día Ingeniería Industrial cuenta con 2 planes académicos, creando la necesidad de realizar una programación específica, ocupando tiempo adicional del personal administrativo. En general, sin importar la practica realizada, la programación de cursos es un proceso tedioso y demorado en el cual se encuentran alumnos sin asignar, y no se sabe si existe una solución factible a esta esta situación.
La propuesta realizada para la creación de una programación semanal sigue varias reglas, algunas de las cuales son tan importantes que nunca pueden ser violadas (restricciones duras), existen otras restricciones las cuales corresponden a la particularidad del programa y generalmente se obedecen solo si se satisfacen todas las restricciones duras y todavía hay espacio para mejores soluciones bajo algunos objetivos para mejorar la calidad (restricciones suaves).
Las restricciones estrictas para el horario universitario están reguladas por las siguientes reglas básicas:
•No se permiten colisiones. En un horario, una colisión ocurre cuando dos o más cursos están programados en el mismo período para el mismo maestro, para el mismo grupo de estudiantes o para la misma aula. Además, cuando dos o más profesores son asignados al mismo grupo de estudiantes para enseñar dos cursos diferentes; y, por último, cuando se asignan dos o más aulas al mismo curso y al mismo grupo de estudiantes.
•El calendario debe estar completo. Un horario se completa cuando todos los cursos planificados para cada grupo de estudiantes aparecen en el horario, con la cantidad correcta de períodos de tiempo para cada curso y cada parte de cada curso. También, cuando a cada miembro del personal docente se le asigna el número total de períodos de enseñanza que la institución requiere.
•El horario debe dar cabida a las solicitudes de sesiones de períodos de enseñanza consecutivos. Dependiendo del curso y del número de períodos de enseñanza asignados por semana, un profesor puede optar por impartir el curso en sesiones de un solo período o de varios períodos. El horario debe poder programar un curso determinado en cualquier esquema que el profesor responsable decida seguir.
•El horario debe tener en cuenta las solicitudes de sesiones repetitivas de un curso determinado o parte de un curso. Esta regla se refiere a la necesidad que presentan algunos cursos de sesiones de recitaciones o trabajos de laboratorio que están diseñados para grupos pequeños. En este caso, la misma sesión debe repetirse varias veces para acomodar el número total de estudiantes registrados.
Del mismo modo, las restricciones suaves para el horario universitario están reguladas por las siguientes reglas de calidad:
•Las preferencias para la enseñanza en intervalos de tiempo específicos se obedecen si es posible. Cada miembro del personal docente puede expresar una preferencia con respecto al período preferido para impartir sus cursos. Por ejemplo, uno puede preferir enseñar un curso determinado durante los períodos de la mañana, mientras que otro durante los períodos de la tarde.
•Los horarios de los estudiantes deben ser lo más compactos posible, sin embargo, permita descansos durante las horas de almuerzo.
4. Modelo Matemático
El modelo matemático para la programación de horarios sigue el enfoque utilizado por Daskalaki et al. (2004). En este caso se utiliza un modelo de programación entera, con variables de decisión estrictamente binarias. A continuación, se hace una descripción de cada uno de los componentes del modelo.
4.1 Subíndices
Para identificar las variables y parámetros se utilizan 7 subíndices que son:
Franja Horaria: indica la hora del día en la que se puede programar un curso. Estas franjas están dividas en intervalos una hora e inician de 7 Am a 8 Am hasta las 5 Pm a 6 Pm.
Asignatura: la asignatura corresponde a un grupo de un curso en particular. Ejemplo, el curso de Investigación de Operaciones I puede tener dos grupos diferentes, por tanto, el subíndice considerará cada grupo separado. Cada semestre se define el número de grupos a ofertar para cada curso, por tanto, el número total de asignaturas a programar puede variar de un semestre otro.
Docentes: son las personas que pueden enseñar las diferentes asignaturas. Si bien la Universidad maneja dos tipos de vinculación para los docentes, el modelo no hace esta distinción.
Días hábiles: son los días de la semana que están habilitados para programar las asignaturas. Por política de la Universidad, se pueden programar asignaturas de lunes a sábados.
Semestre al que pertenece la asignatura: corresponde al semestre, según el currículo del programa, en el que se encuentra ubicado el curso.
Bloques de franjas horarias de dos horas o tres horas: por política de la facultad las sesiones de clase para una asignatura se pueden programas en bloques de dos o tres horas. De esta manera si un curso tiene una intensidad horaria de cuatro horas por semana, se deben programar dos sesiones por semanas en bloques de horas. De otro lado, si un curso tiene una intensidad horaria de tres horas por semana, se puede programar una sola sesión por semana en un bloque de tres horas. En la Figura 2 se presenta la definición de los bloques de dos y tres horas en la relación a las franjas horarias.
Figura 2. Ubicación de los bloques 2 y 3 horas en las franjas horarias
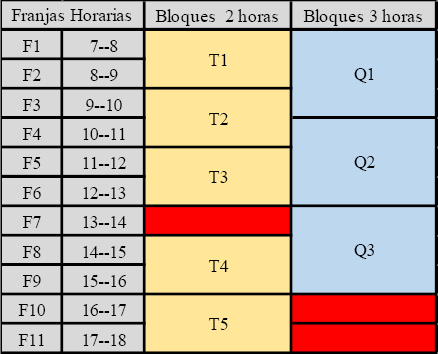
Fuente: Elaboración propia
En la Tabla 1 se presenta un resumen de los subíndices que se utilizarán en el modelo.
Tabla 1. Descripción de subíndices del modelo matemático
|
Subíndice |
Descripción |
|
i |
Franjas Horarias |
|
j |
Asignatura |
|
k |
Docentes |
|
n |
Días hábiles |
|
m |
Semestre al que pertenece una asignatura |
|
t |
Bloques de franjas horarias de dos horas |
|
q |
Bloques de franjas horarias de tres horas |
Fuente: Notación adaptada del modelo IP en (Torres-Ovalle et al., 2014)
4.2 Variables de decisión
Se utiliza un total de cuatro variables binarias. La primera consiste en la variable de decisión principal Xijkn , la cual toma el valor de 1 si en la franja horaria i se asigna la asignatura j al docente k en el día n. Además, se utilizan un grupo de variables auxiliares que ayudan a tomar decisiones de asignación y programación. En primer lugar se utiliza la variable Yjk , la cual toma el valor de 1 para asignar el docente k a la asignatura j. La variable Hjknt , toma el valor de 1 si la asignatura j dictada por el docente k en el día n es programada en el bloque de dos horas t. La variable Gjknq, toma el valor de 1 si la asignatura j dictada por el docente k en el día n es programada en el bloque de tres horas q. Las dos últimas variables auxiliares permiten que la programación de una asignatura en un día en particular se realice en bloques de dos o tres horas consecutivas.
4.3. Parámetros
Los parámetros se definieron teniendo en cuenta las políticas y características de la Universidad y el programa con respecto a los cursos, los profesores, la capacidad instalada y el currículo del programa. A continuación, se listan los parámetros del modelo:
•INTHj: Número de franjas horarias que se deben dictar de forma presencial, semanalmente, de la asignatura j.
•PMAXk: Número de franjas horarias que puede dictar como máximo, el docente k, a la semana.
•PMINk: Número de franjas horarias que debe dictar como mínimo, el docente k, a la semana.
•DOSFj: Parámetro binario que toma el valor 1 si la asignatura j se dicta en bloques de dos horas y 0 de lo contrario.
•TRESFj: Parámetro binario que toma el valor 1 si la asignatura j se dicta en bloques de tres horas y 0 de lo contrario.
•MSjm: Parámetro binario que toma el valor 1 para indicar que la asignatura j pertenece al semestre m y 0 de lo contrario.
•MPjk: Parámetro binario que toma el valor 1 para indicar que la asignatura j puede ser asignada al docente k y 0 de lo contrario.
•FPnik: Parámetro binario que toma el valor 1 para indicar que el docente k está disponible el día n en la franja i y 0 de lo contrario.
•MSF: es un escalar que indica el máximo de salones disponibles por franja horaria
•CFMnij: es el costo estimado de “insatisfacción” al asignar la asignatura j en el día n en la franja i.
4.4 Función objetivo y restricciones
El objetivo del modelo es minimizar el costo total estimado de insatisfacción de acuerdo a una programación dada. Esto se encuentra representado en la ecuación (1).
Función objetivo:
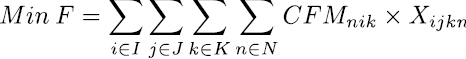
Restricciones:
(12),(13), (14), (19), (24), (25)
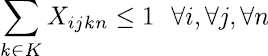

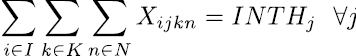
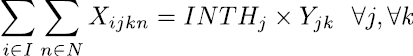
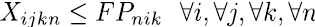
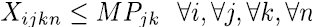
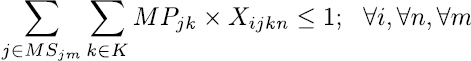
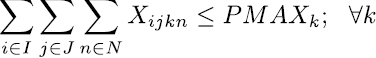
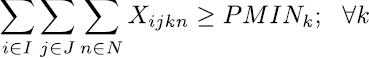
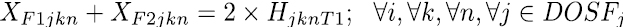
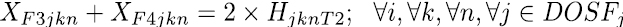
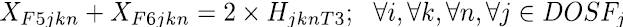
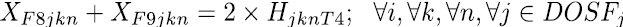
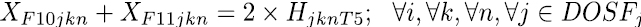
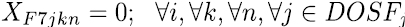


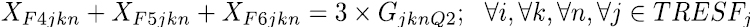
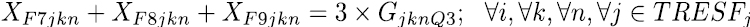
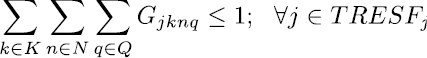
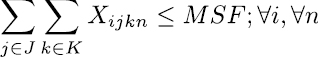
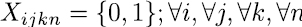
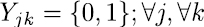
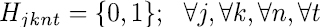
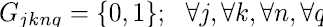
El modelo considera inicialmente las restricciones duras del modelo, están son las que se deben tener en cuenta tal y como están a la hora de modelar. Las ecuaciones (2) y (4) son restricciones que aseguran que no se lleven conflictos a la construcción de los horarios, la ecuación (2) asigna un curso a un docente en una franja horaria y día, la ecuación (4) determina que cada asignatura solo sea asignada como máximo una vez en un respectivo día y franja horaria dictada por un docente.
Las ecuaciones (4) a (6) se conocen como restricciones de completitud, establece que toda asignatura sea programada según su intensidad horaria semanal, la ecuación (5) se encarga que cada asignatura solo sea dictada por un único docente, esto significa que, si una asignatura se da en tres momentos diferentes de la semana, en los tres momentos la clase sea dictada por el mismo docente y no que en alguno de los momentos asigne un docente diferente para la asignatura. La restricción indicada en la ecuación (6) establece que un docente solo sea asignado para dictar una asignatura en un respectivo día y franja horaria, si cuenta con la disponibilidad requerida, las ecuaciones (7) se encargan de asignar los docentes con las habilidades requeridas.
Las restricciones blandas, se utilizan para dirigir los coeficientes de costo en la función objetivo, su objetivo es llevar la solución final a horarios de mayor calidad. La expresión de la ecuación (8) se encarga que las asignaturas definidas como pertenecientes a un mismo semestre se programen en diferentes momentos, es decir en diferente día o franja. La restricción (9) y (10) establece los limites inferiores y superiores de carga horaria semanal para cada docente, las ecuaciones (11) a (15) se encargan de asignar, para las asignaturas que se dictan en bloques de dos horas, franjas horas de forma consecutiva, en este sentido la restricción (17) selecciona uno de los cinco bloques de dos horas disponibles para cada día y la restricción (16) bloquea la franja 7 que va de 1 Pm – 2 Pm. De igual manera ocurre con las asignaturas que se dictan en bloques de tres horas, en este caso las restricciones (18) a (20) realizan las asignaciones de las franjas horarias de forma consecutiva y la restricción (21) hace la selección de uno de los tres bloque de tres horas disponibles para cada día.
La expresión de la ecuación (22) se encarga de que se respete el límite de salones permitidos por franja horaria para el Programa de acuerdo con lo estipulado por la Universidad. Por último, las restricciones (23) a (26) indican el dominio de las variables de decisión y auxiliares.
5. Caso de Aplicación
5.1 Datos de Entrada
El modelo se ejecutó con los parámetros para la planeación de horarios en un semestre académico. Los resultados se compararon con la programación manual realizada por el programa para ese mismo semestre. En la Tabla 2 se presenta un resumen de los parámetros utilizados y a continuación una descripción.
Franjas horarias: de acuerdo a los lineamientos establecidos por la Facultad de Ingeniería para la programación de todos los cursos de sus programas, para cada día se definieron 11 franjas horarias dividas en intervalos de tiempo de una hora, desde las 7:00 Am hasta las 6:00 Pm.
Días hábiles: Por lineamientos de la Universidad los cursos deben programarse entre lunes y sábados, por tanto, se tendrán disponible 6 días hábiles para realizar la programación de los horarios.
Asignaturas: Se programaron 90 cursos los cuales están a cargo del programa de Ingeniería Industrial, excluyendo los cursos de ciencias básicas (cálculos, físicas, química, probabilidad y estadística), ciencias sociales, humanidades y los cursos que toman los estudiantes del programa pero que son impartidos por otros programas de la Facultad de Ingeniería y otras Facultades. De las 90 asignaturas a programar 61 % (55 asignaturas) corresponden a las asignaturas dictadas en bloques de 3 horas y el 39 % restante (35 asignaturas) que corresponden a los bloques de 2 horas.
Docentes: En este semestre se tiene una disponibilidad de 30 docentes, los cuales se dividen entre docentes de tiempo completo (fijos) y docentes de cátedra (temporales).
Semestre: El currículo del Programa de Ingeniería Industrial tiene una duración de 10 semestres académicos y en cada uno de estos hay asignaturas que se imparten desde el programa.
Tabla 2. Subíndices del modelo matemático
|
Subíndice |
Descripción |
Dominio |
|
i |
Franjas Horarias |
i = 1,2,…,11 |
|
j |
Asignatura |
j = 1,2,…,90 |
|
k |
Docentes |
k = 1,2,…,29 |
|
n |
Días hábiles |
n = 1,2,…,6 |
|
m |
Semestre al que pertenecer una asignatura |
m = 1,2,…,10 |
|
t |
Bloques de franjas horarias de dos horas |
t = 1,2,…,5 |
|
q |
Bloques de franjas horarias de tres horas |
q = 1,2,3 |
La matriz CFM se pondera con valores entre 1 y 12, los cuales se manejan en una escala que se describe en la Tabla 3.
Tabla 3. Escala de la matriz CFM
|
Costo |
Criterio |
|
1 a 2 |
Muy deseado |
|
3 a 4 |
Deseado |
|
5 a 6 |
Aceptable |
|
7 a 8 |
Poco deseado |
|
9 a 10 |
No deseado |
|
11 a 12 |
Altamente no deseado |
Fuente: Elaboración propia
5.2. Desempeño del Modelo
El modelo se programó en el lenguaje de modelado y programación matemática GAMS (General Algebraic Modeling Language), con el Solver Coin Branch & Cut CBC en un computador Lenovo 10B7A2AH00 con un procesador CORE i5 4590 y una memoria de 4GB.
El modelo fue ejecutado exitosamente teniendo un tiempo de generación de 117,456 segundos (32.6 horas apróx.). El modelo ejecutó 284.079.116 iteraciones. El costo total obtenido para este horario fue de 1668 unidades (Solución Final). (Para consultar los datos y el modelo puede cnsultar el repositorio GitHub mediante el siguiente enlace https://github.com/hfelizzola/Timetabling-Unisalle) En contraste con la solución manual que tomo un tiempo de 40 horas y su función objetivo de 2073 unidades, generando una reducción de 405 unidades equivalentes al 19.5 %.
5.3 Distribución de la Carga Horaria por Día
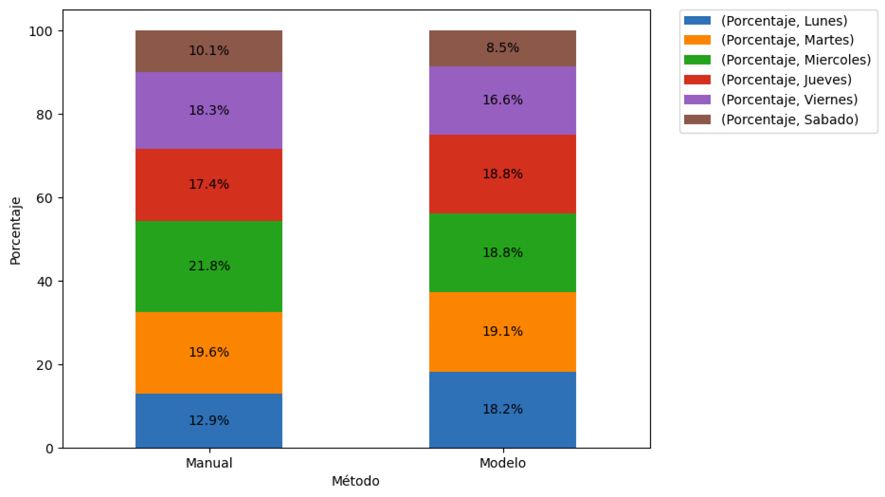
En la Figura 3 se presenta la distribución porcentual de la carga de horas programadas por día de acuerdo al método utilizado para la programación. Se observa que ambas distribuciones son similares presentando cerca del 90 % de las horas programas entre los días lunes y viernes y cerca del 10 % restante los días lunes y sábado, esto se debe a la prioridad del Programa de Ingeniería Industrial de programar la mayoría de asignaturas de lunes a viernes exceptuando algunas muy específicas. La baja carga de los días lunes, en la programación manual, se debe a dos causas principales: la primera es que este día cuenta con las franjas horaria de 11:00 a 13:00 restringidas ya que se destinan en algunos casos para reuniones de los profesores y los comités del Programa y la segunda es que por política del Programa se prefiere evitar asignación de asignaturas con bloques de horas, ya que en Colombia gran parte de los días festivos se dan los días lunes, lo cual afecta significativamente el cumplimiento de las clases que se programan en este horario. En contraste el modelo matemático asigna un mayor porcentaje de horas los días lunes en comparación a la solución, y menor porcentaje de los días sábados. En la solución manual el mayor porcentaje de franjas asignadas se da el día miércoles y con el modelo matemático el día martes.
Figura 3. Distribución porcentual de la carga de horas programadas por métodos y día
Fuente: Elaboración propia
Nota El método manual hace referencia al método heurístico utilizado por el Programa para realizar la programación semestral. El Modelo corresponde al modelo matemático que se presenta en el artículo.
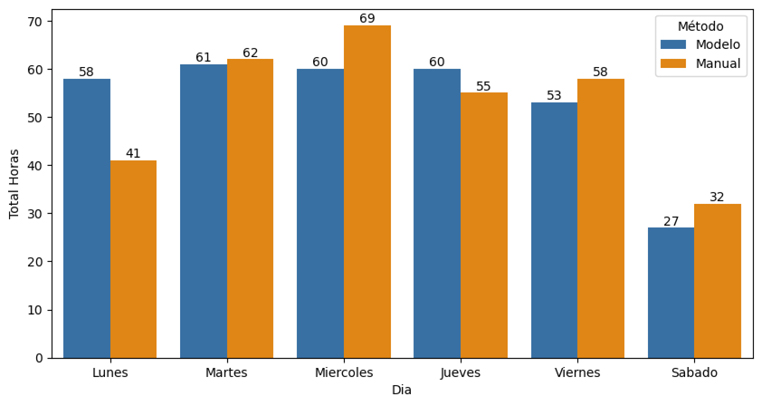
En la Figura 4 se puede observar qué el modelo matemático se tiene una distribución uniforme de la carga entre los días lunes y jueves las cuales se mantienen entre 58 y 60 horas, en contraste la solución manual tiene diferencias porcentuales significativas entre estos mismos días, variando de un mínimo de 41 horas el día lunes a un máximo de 69 horas el día miércoles.
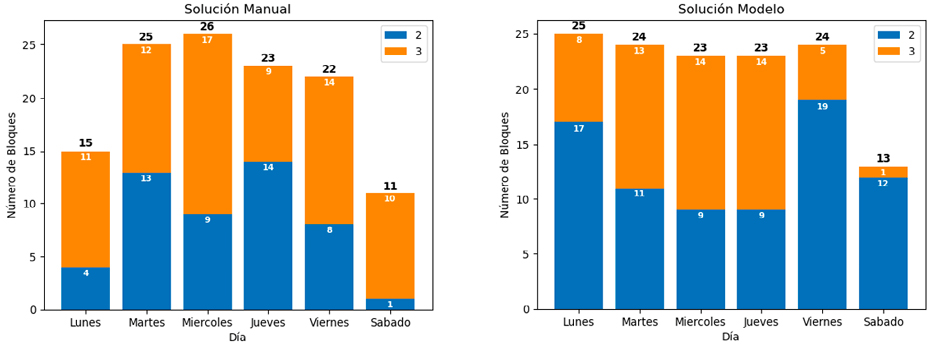
Adicionalmente, en la Figura 4 se puede identificar que a pesar de que hay un predominio en la cantidad de las asignaturas de 3 horas, en cuanto a intensidad horaria se presenta un equilibrio debido a que las asignaturas de 3 horas se dictan una vez a la semana y las asignaturas programadas en bloques de 2 horas se pueden llegar a programar hasta 3 veces a la semana. El modelo debe garantizar que se mantenga el equilibrio al momento de asignar las materias de 2 y 3 horas, según corresponda, de la manera más eficiente posible, siendo éste uno de los mayores desafíos que enfrenta la universidad en este campo. Adicionalmente, se debe tener en cuenta que la cantidad máxima de salones disponibles por franja (parámetro MSF), es de 9 aulas. Una diferencia fundamental, es que el modelo intenta programar menos bloques de tres horas los días sábados, viernes y lunes respectivamente. Esto podría tener beneficios desde el punto de vista pedagógico y administrativo, ya que, por un lado los días viernes y sábados al estar al final de la semana puede ser preferible dictar cursos en bloques de dos horas con respecto a tres horas, además, a tener una menor cantidad de bloques de tres horas los días lunes, puede evitar una mayor pérdida de clase debido a los días festivos, que en su mayoría se ubican los días lunes. En la solución manual estos bloques de tres horas se programan de forma uniforme durante toda la semana.
Figura 4. Distribución de la carga de horas programadas por día
Fuente: Elaboración propia
Figura 5. Bloques programados por día
Fuente: Elaboración propia
5.4 Distribución de la Carga Horaria por Franja
En la Figura 6 se presenta la distribución de la cantidad de horas semanales programadas en cada franja horaria para la solución manual y la solución obtenida con el modelo. En la solución entregada por el modelo se puede observar que la mayor carga horaria se da en las franjas de 7:00 Am a 9:00 Am, esto se debe a que es el horario preferido por profesores de cátedra para dictar clases debido a las restricciones que existe para dictar clases en horario nocturno. En la jornada de la tarde la mayor carga horaria se concentra entre las 2:00 Pm y 4:00 Pm. Por otro lado, no se realizan programaciones entre la 1:00 Pm y 2:00 Pm, la cual se espera se destine para el almuerzo y únicamente está disponible para asignaturas que se dictan en bloques de 3 horas. Otra franja donde no se programaron clase es de 5:00 Pm a 6:00 PM, que es un horario de baja preferencia tanto de docente de cátedra como de planta. La diferencia significativa entre las dos soluciones se da en la carga de horas en la tarde, ya que, la solución manual tiene una mayor carga en horas de en comparación a la solución del modelo, la cual programa un 50 % menos de horas en total.
Figura 6. Horas Programadas por Franja
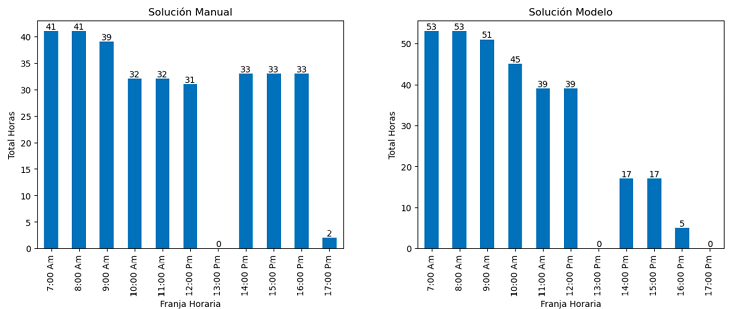
Fuente: Elaboración propia
Si analizamos la distribución de la carga de horas por franja de horas y día en la solución del modelo (ver Figura 7) podemos observar que es similar de lunes a viernes para las jornadas de mañana y tarde, y cambia significativamente para los días lunes en la tarde donde la jornada de la mañana desciende la carga significativamente a partir de las 11:00 Am. Por otro lado, el día sábado tiene una carga significativamente menor a los demás días, lo cual es lógico debido a la baja preferencia que se tiene para en la programación. En la solución manual la programación en horas de la tarde cambia significativamente entre semana, variando de 3 horas el día lunes a 9 horas los días martes. Además, se pueden se pueden observar variaciones leves en la jornada de la mañana. Las dos soluciones tienen en común que no se programan horas los sábados en tarde.
Figura 7. Programación por Día y Franja Horaria
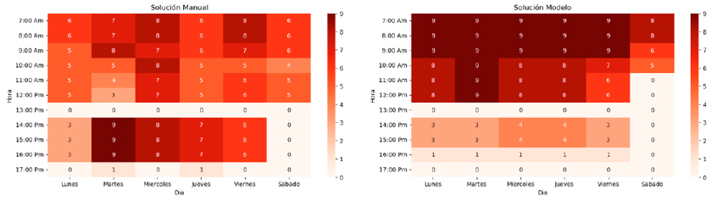
Fuente: Elaboración propia
6. Conclusiones
Con el desarrollo e implementación del modelo matemático para la programación de horarios se logran impactos positivos ya que se convierte en la base para automatizar dicha tarea y con esto reducir los tiempos necesarios para su realización. En sentido, el modelo mostró gran efectividad para realizar una programación factible y en tiempo razonable a pesar de ser un problema de alta complejidad debido a las múltiples restricciones que se presentan. Se validó el modelo a través de la comparación de los resultados obtenidos, para un semestre académico, con la programación real realizada por el Asistente Académico. Se encontró cierto nivel de similitud en los horarios académicos.
La solución del modelo en GAMS tomó un tiempo de 32 horas comparado con el tiempo que tomó la programación manual que tomó 40 horas. La implementación de este modelo implica no sólo la reducción del tiempo para tener una solución, sino que se logra liberar horas administrativas para la elaboración del horario el cual puede ser destinado para otras actividades. Adicionalmente, el modelo permite evaluar escenarios, cambio de política, cambios de capacidad y en general incluir modificaciones con relativa facilidad.
Una revisión de literatura inicial permitió establecer las técnicas matemáticas utilizadas para la realización de horarios académicos entre las cuales estaban programación lineal entera mixta y técnicas heurísticas, sin embargo, el uso de técnicas heurísticas se remitía a instancias grandes. En general, se encontraron restricciones en común entre los diferentes trabajos desarrollados relacionadas con: la disponibilidad del docente, el respeto de los horarios definidos por las instituciones académicas y las limitaciones del espacio físico. Sin embargo, también se identifica que cada entorno académico tiene restricciones particulares las cuales pueden ser de orden académico o administrativo las mismas, llevan a una modificación de las restricciones básicas y a las necesidades de generar nuevas restricciones para el sistema.
La principal dificultad que se tuvo para el diseño del modelo fue cumplir con la distribución de las asignaturas en las franjas horarias de disponibilidad del Programa de Ingeniería Industrial, debido a que se manejaron dos tipos de asignaturas: las dictadas en bloques de dos horas y en bloques de tres horas. Para dar solución a esta situación se definieron restricciones diferentes para cada tipo de asignatura, donde se limitaba la disponibilidad de franjas horarias. El modelo final obtenido para el Programa de Ingeniería Industrial cuenta con una función objetivo y un total de 23 restricciones, para su elaboración se tomó como principal referencia, el modelo de (Torres-Ovalle et al., 2014), de este modelo se adaptó la función objetivo y alrededor del 17,39 % de las restricciones.
En contraste con la solución manual que tomo un tiempo de 36 horas y su función objetivo de 2073 unidades, generando una reducción de 405 unidades equivalentes al 19.5 %.
REFERENCIAS
& (2021). Genetic Algorithm For Solving University Course Timetabling Problem Using Dynamic Chromosomes. 2021 International Conference of Technology, Science and Administration (ICTSA), 1-6. https://doi.org/10.1109/ICTSA52017.2021.9406539
& (2015). Mathematical models and algorithms for a high school timetabling problem. Computers & Operations Research, 61, 56-68. https://doi.org/10.1016/j.cor.2015.02.011
(2008). Fuzzy Methodologies for Automated University Timetabling Solution Construction and Evaluation [PhD Thesis]. University of Nottingham.
, & (2018). Genetic Algorithm Analysis using the Graph Coloring Method for Solving the University Timetable Problem. Procedia Computer Science, 126, 899-906. https://doi.org/10.1016/j.procs.2018.08.024
, & (2015). A survey of approaches for university course timetabling problem. Computers & Industrial Engineering, 86, 43-59. https://doi.org/10.1016/j.cie.2014.11.010
, & (1998). Integrated Airline Schedule Planning. En G. Yu (Ed.), Operations Research in the Airline Industry (Vol. 9, pp. 384-403). Springer US. https://doi.org/10.1007/978-1-4615-5501-8_13
& (1994). The Reactive Tabu Search. ORSA Journal on Computing, 6(2), 126-140. https://doi.org/10.1287/ijoc.6.2.126
, , , & (1999). Resource-constrained project scheduling: Notation, classification, models, and methods. European Journal of Operational Research, 112(1), 3-41. https://doi.org/10.1016/S0377-2217(98)00204-5
, & (2016). Workforce scheduling and routing problems: Literature survey and computational study. Annals of Operations Research, 239(1), 39-67. https://doi.org/10.1007/s10479-014-1687-2
, & (2012). Design, engineering, and experimental analysis of a simulated annealing approach to the post-enrolment course timetabling problem. Computers & Operations Research, 39(7), 1615-1624. https://doi.org/10.1016/j.cor.2011.09.014
, & (2004). An integer programming formulation for a case study in university timetabling. European Journal of Operational Research, 153(1), 117-135. https://doi.org/10.1016/S0377-2217(03)00103-6
& (2001). Optimal timetables for public transportation. Transportation Research Part B: Methodological, 35(8), 789-813. https://doi.org/10.1016/S0191-2615(00)00023-0
(1985). An introduction to timetabling. European Journal of Operational Research, 19(2), 151-162. https://doi.org/10.1016/0377-2217(85)90167-5
& (2001). Implementation of a university course and examination timetabling system. European Journal of Operational Research, 130(1), 202-213. https://doi.org/10.1016/S0377-2217(00)00052-7
& (2016). A MILP model for the teacher assignment problem considering teachers’ preferences. European Journal of Operational Research, 249(3), 1153-1160. https://doi.org/10.1016/j.ejor.2015.08.057
, & (2012, septiembre 27). A Survey of Approaches for University Course Timetabling Problem. Proceedings of 8th International Symposium on Intelligent and Manufacturing Systems (IMS 2012).
, & (2017). An integer program and a hybrid genetic algorithm for the university timetabling problem. Optimization Methods and Software, 32(3), 625-649. https://doi.org/10.1080/10556788.2016.1233970
(2008). Particle swarm optimization with an improved exploration-exploitation balance. 2008 51st Midwest Symposium on Circuits and Systems, 759-762. https://doi.org/10.1109/MWSCAS.2008.4616910
, & (2019). Simulated annealing with improved reheating and learning for the post enrolment course timetabling problem. Journal of the Operational Research Society, 70(6), 873-888. https://doi.org/10.1080/01605682.2018.1468862
(1962). The Construction of Class-Teacher Time-Tables. Information Processing, Proceedings of the 2nd IFIP Congress 1962, Munich, Germany, August 27 - September 1, 1962, 73-77.
& (2020). Robust university course timetabling problem subject to single and multiple disruptions. European Journal of Operational Research, 283(2), 630-646. https://doi.org/10.1016/j.ejor.2019.11.024
& (1993). Multiple-shift Workforce Scheduling under the 3-4 compressed workweek with a Hierarchical Workforce. IIE Transactions, 25(5), 82-89. https://doi.org/10.1080/07408179308964318
, & (2007). A multiobjective faculty–course–time slot assignment problem with preferences. Mathematical and Computer Modelling, 46(7-8), 1017-1029. https://doi.org/10.1016/j.mcm.2007.03.012
, , , , , , & (2022). An Enhanced Particle Swarm Optimization for ITC2021 Sports Timetabling. Computers, Materials & Continua, 72(1), 1995-2014. https://doi.org/10.32604/cmc.2022.025077
& (2012). Appointment Overbooking in Health Care Clinics to Improve Patient Service and Clinic Performance. Production and Operations Management, 21(5), 874-888. https://doi.org/10.1111/j.1937-5956.2011.01308.x
(2012). A time-dependent metaheuristic algorithm for post enrolment-based course timetabling. Annals of Operations Research, 194(1), 273-289. https://doi.org/10.1007/s10479-010-0696-z
, , , & (2012). A new model for automated examination timetabling. Annals of Operations Research, 194(1), 291-315. https://doi.org/10.1007/s10479-011-0997-x
(2018). Random partial neighborhood search for the post-enrollment course timetabling problem. Computers & Operations Research, 90, 84-96. https://doi.org/10.1016/j.cor.2017.09.014
(2019). A Study on Course Timetable Scheduling and Exam Timetable Scheduling using Graph Coloring Approach. International Journal for Research in Applied Science and Engineering Technology, 7(3), 1999-2006. https://doi.org/10.22214/ijraset.2019.3368
, & (2003). Project Scheduling with Time Windows and Scarce Resources: Temporal and Resource-Constrained Project Scheduling with Regular and Nonregular Objective Functions. Springer Berlin Heidelberg. http://public.ebookcentral.proquest.com/choice/publicfullrecord.aspx?p=3087342
, , & (2012). Solving the post enrolment course timetabling problem by ant colony optimization. Annals of Operations Research, 194(1), 325-339. https://doi.org/10.1007/s10479-012-1078-5
& (2010, junio). A two phase integer linear programming approach to solving the school timetable problem | IEEE Conference Publication | IEEE Xplore. Proceedings of the ITI 2010, 32nd International Conference on Information Technology Interfaces. https://ieeexplore.ieee.org/abstract/document/5546473?casa_token=8NXEYLyhBJYAAAAA:DO9jDMq4-wyY2YxPPgfUUOGBO1n4ELugtWtLZzG3WTMrYB09TAvcnX6Nkr2N0KKYHvBoQ7CY0Ect7VU
, & (2007). Modelos de Programación Entera para un Problema de Programación de Horarios para Universidades. Ingeniare. Revista Chilena de Ingeniería, 15(3). https://doi.org/10.4067/S0718-33052007000300005
, & (2017). Review of energy-efficient train control and timetabling. European Journal of Operational Research, 257(2), 355-376. https://doi.org/10.1016/j.ejor.2016.09.044
(1988). Split Vertices in Vertex Colouring and Their Application in Developing a Solution to the Faculty Timetable Problem. The Computer Journal, 31(1), 76-82. https://doi.org/10.1093/comjnl/31.1.76
, & (2021). A multi-objective optimisation model for train scheduling in an open-access railway market. Transportation Planning and Technology, 44(2), 176-193. https://doi.org/10.1080/03081060.2020.1868085
& (2013). Metaheuristics. En S. I. Gass & M. C. Fu (Eds.), Encyclopedia of Operations Research and Management Science (pp. 960-970). Springer US. https://doi.org/10.1007/978-1-4419-1153-7_1167
, , & (2021). A survey of the state-of-the-art of optimisation methodologies in school timetabling problems. Expert Systems with Applications, 165, 113943. https://doi.org/10.1016/j.eswa.2020.113943
, , , & (2014). University Course Scheduling and Classroom Assignment. Ingenieria y Universidad, 18(1), 59-76. https://doi.org/10.11144/Javeriana.IYU18-1.phaa
, , & (2016). Developing compact course timetables with optimized student flows. European Journal of Operational Research, 251(2), 651-661. https://doi.org/10.1016/j.ejor.2015.11.028
& (2019). Multi-train trajectory optimization for energy-efficient timetabling. European Journal of Operational Research, 272(2), 621-635. https://doi.org/10.1016/j.ejor.2018.06.034
(1967). An upper bound for the chromatic number of a graph and its application to timetabling problems. The Computer Journal, 10(1), 85-86. https://doi.org/10.1093/comjnl/10.1.85
(2002). Initial Planning for Urban Transit Systems. En W. H. K. Lam & M. G. H. Bell (Eds.), Advanced Modeling for Transit Operations and Service Planning (pp. 1-29). Emerald Group Publishing Limited. https://doi.org/10.1108/9780585475226-001
& (2014). Appointment Scheduling with No-Shows and Overbooking. Production and Operations Management, 23(5), 788-801. https://doi.org/10.1111/poms.12065
, & (2021). School Timetabling Optimisation Using Artificial Bee Colony Algorithm Based on a Virtual Searching Space Method [Preprint]. Mathematics and Computer Science. https://doi.org/10.20944/preprints202111.0215.v1